Toistomittausten varianssianalyysi

Päivitetty 25.4.2019.

Jos tarkoituksena on tutkia aiheuttavatko käsittelyt eroja tutkittavien ominaisuuksiin, niin keskeisimmät tutkimusasetelmat ovat:

Satunnaistettu koe (completely randomized design): Jokaista käsittelyä varten arvotaan oma ryhmä tutkittavia. Tällöin analyysimenetelmänä käytetään yksisuuntaista varianssianalyysiä.

Toistomittaus (repeated measures design): Käytetään samaa tutkittavien joukkoa eri käsittelyillä. Tätä kutsutaan toistomittaukseksi, koska samoja tutkittavia mitataan toistuvasti eri käsittelyillä. Tällöin analyysimenetelmäksi sopii toistomittausten varianssianalyysi. Esimerkiksi kolmen erilaisen moottorin säädön vaikutusta polttoaineen kulutukseen voidaan tutkia kuuden eri kuljettajan avulla siten, että kukin kuljettaja ajaa testilenkin jokaisella säädöllä. Mittaus toistetaan siis kullekin kuljettajalle 3 kertaa, mutta jokaisella kerralla on erilainen säätö.

Satunnaistettu lohkokoe (randomized block design): Jos tiedetään, että jokin tutkittavien ominaisuus vaikuttaa mittauksen kohteena oleviin muuttujiin, niin tutkittavat voidaan jakaa kyseisen ominaisuuden mukaan samanlaisiin lohkoihin. Esimerkiksi samaan pikaruokaketjuun kuuluvien neljän ravintolan eroja voidaan arvioida jakamalla arvioijat kokemuksen mukaan kuuteen eri lohkoon seuraavasti:

• ensimmäiseen lohkoon otetaan vain kaikkein kokeneimmat arvioijat
• toiseen lohkoon otetaan hieman vähemmän kokeneet arvioijat jne.
• kuudenteen lohkoon otetaan kaikkein vähiten kokemusta omaavat arvioijat
• kuhunkin lohkoon otetaan neljä arvioijaa, koska arvoitavia ravintoloita on neljä
• samaan lohkoon kuuluville neljälle arvioijalle arvotaan satunnaisesti arvioitavat ravintolat.

Asetelmalla pyritään kontrolloimaan arvioijan kokemuksen vaikutusta arvioihin. Myös tähän asetelmaan sopii analyysimenetelmäksi toistomittausten varianssianalyysi.

Yksisuuntaisen varianssinalyysin ja toistomittausten varianssianalyysin keskeinen ero

Yksisuuntaisessa varianssianalyysissä mittaustulosten vaihtelu jaetaan ryhmien (kutakin käsittelyä vastaa yksi ryhmä) väliseen ja ryhmien sisäiseen vaihteluun. Kyseessä on malli, jossa pyritään selittämään vaihtelu ryhmien (käsittelyjen) eroilla ja tässä mallissa kaikki muu kuin ryhmien välinen vaihtelu on luettavissa virhevaihteluksi.

Toistomittausten varianssianalyysissä erotetaan ryhmien sisäisestä vaihtelusta lohkojen välinen vaihtelu ja muu osa ryhmien sisäisestä vaihtelusta luetaan virhevaihteluksi. Kyseessä on malli, jossa pyritään selittämään vaihtelu ryhmien eroilla ja lohkojen eroilla. Muu kuin ryhmien välinen ja lohkojen välinen vaihtelu luetaan virhevaihteluksi. Virhevaihtelu jää pienemmäksi kuin yksisuuntaisessa varianssianalyysissä, koska lohkojen välinen vaihtelu otetaan malliin mukaan.

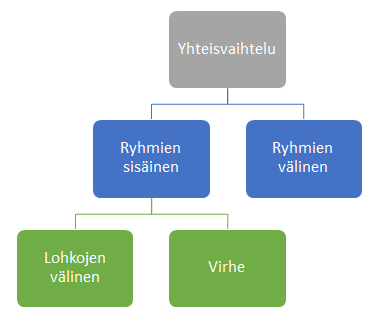
Ryhmien välisten erojen merkitsevyyttä mitataan ryhmien välisen vaihtelun ja virhevaihtelun suhteena. Jos ryhmien vaihtelu on riittävän paljon virhevaihtelua suurempi, niin sillon ryhmien välisiä eroja voidaan pitää merkitsevinä. On siis olennaista, että käytetään mallia, jossa virhevaihtelu saadaan mahdollisimman pieneksi. Näin ollen toistomittausasetelmassa ja satunnaistetussa lohkoasetelmassa kannatta aina käyttää toistomittausten varianssianalyysiä yksinkertaisen varianssianalyysin sijasta.

Toistomittausten varianssianalyysi Excelillä

Esimerkki. Auton polttoaineen kulutusta verrattin kolmella erilaisella moottorin säädöllä A, B ja C. Testikuljettajina oli 6 kuljettajaa, jotka ajoivat arvotussa järjestyksessä testilenkin kullakin säädöllä. Mitatut kulutukset (litraa sadalla kilomertrilla) olivat oheisen taulukon mukaiset.

Excelin analyysityökalujen avulla voin laskea toistomittausten varianssianalyysin. Jos et ole aiemmin ottanut analyysityökaluja käyttöön, niin voit tehdä sen seuraavasti:

• Valitsen File – Options (Tiedosto – Asetukset).
• Valitsen Add Ins (Apuohjelmat) ja valitsen alhaalta Manage (Hallinta) -ruudusta Excel Add Ins (Excel-apuohjelmat).
• Valitsen Go (Siirry).
• Valitsen luettelosta Analysis Toolpak (Analyysityökalut) ja valitsen OK.
• Tämän jälkeen löydän Data (Tiedot) -välilehdeltä analyysityökalut (Data Analysis).

Analyysityökaluista löydän toistomittausten varianssianalyysin nimellä Anova: Two-Factor Without Replication (Anova: kaksisuuntainen ilman toistoa). Nimitys kaivannee hieman selitystä: ’kaksisuuntainen’ viittaa siihen, että yhteisvaihtelua selitetään kahdella tekijällä, käsittelyllä ja tutkittavien/lohkojen eroilla; ’ilman toistoa’ viittaa siihen, että kullakin käsittelyn ja tutkittavan/lohkon yhdistelmällä on vain yksi mittaus.

Täytän Anova-ikkunaan syöttöalueen (Input Range). Syöttöalueeksi valitsen kaikki kulutukset sekä rivi- ja sarakeotsikot. Lisäksi määritän, että otsikot huomioidaan (Labels).

Excel tulostaa keskiarvot ja varianssit sekä ANOVA-taulukon, joka näyttää seuraavalta:

ANOVA-taulukossa vaihtelu on jaettu kolmeen osaan:

• rivien eli tässä tapauksessa kuljettajien väliseen vaihteluun (SS=0,55205)
• sarakkeiden eli tässä tapauksessa säätöjen väliseen vaihteluun (SS=0,573333)
• muuhun vaihteluun eli virhevaihteluun (SS=0,196067).

Mitä suurempi säätöjen välinen vaihtelu on virhevaihteluun verrattuna, sitä merkitsevämpiä eroja säätöjen välillä on. Tämä testataan F-testillä, jonka p-arvon voin lukea taulukosta.

Esimerkin tapauksessa ainakin kahden säädön välillä on merkitsevä ero (p-arvo 0,001).

On opettavaista ainakin kerran tutustua ANOVA-taulukon johtamiseen ja erityisesti vaihtelua mittaavien neliösummien (SS, sum of squares) laskemiseen. Voit tutustua ANOVA-taulukon johtamiseen Excel-tiedoston anovakaavat.xlsx avulla. Olen laskenut tiedostoon Excelin kaavoilla kaikki ANOVA-taulukossa oleva luvut. Tiedostosta löytyy laskettu esimerkki myös satunnaistetusta lohkokokeesta.

Käyttöedellytykset

Toistomittausten varianssianalyysiä koskee sama käyttöedellytys kuin muitakin keskiarvon käyttöön perustuvia menetelmiä: otoskeskiarvojen täytyy olla peräisin likimain normaalijakaumasta. Jos ryhmät ovat isoja (vähintään 30), niin normaalijakautuneisuus ei yleensä ole ongelma. Jos ryhmät ovat pieniä, voin arvioida normaalijakautuneisuutta otoksen arvojen jakauman perusteella (histogrammi, ruutu- ja janakaavio). Epäselvissä tapauksissa kannattaa testata normaalijakautuneisuus SPSS:llä. Ohjeet laatikkokaavion tekemiseen ja normaalijakautuneisuuden testaamiseen löydät artikkelistani SPSS: Explore.

Toisena käyttöedellytyksenä on niin kutsuttu sfäärisyys (sphericity). Yksinkertaistaen voisi todeta, että tässä on kyse ryhmien välisten erojen varianssien yhtäsuuruudesta. Sfäärisyyden testaamiseen ei ole toimintoa Excelissä. Lue lisää artikkelista SPSS: Toistomittausten varianssianalyysi.

Jos käyttöedellytykset eivät täyty, niin voin käyttää SPSS:n Friedman-testiä.

Parivertailut

Varianssianalyysi kertoo onko ryhmien keskiarvojen välillä merkitseviä eroja. Sen sijaan varianssianalyysi ei kerro minkä ryhmien välillä on merkitseviä eroja. Arvailuja voin tehdä ryhmien keskiarvojen perusteella. Tarkempaan analyysiin tarvitsen parivertailuja. Excel ei tarjoa valmiita työkaluja parivertailujen tekemiseen. SPSS sisältää menetelmiä parivertailujen tekemiseen. Lue lisää artikkelista SPSS: Toistomittausten varianssianalyysi.