SpecialCells

Tämän artikkelin esimerkit tiedostossa specialcells.xlsm

Range.SpecialCells

Range.SpecialCells-menetelmä vastaa Excelin Home (Aloitus) -välilehden  Find – Go To Special (Etsi – Siirry määräten) -toimintoa. Jollei toiminto ole tuttu, niin kannattaa tutustua. Toiminnon käyttöä VBA:n puolella voit opetella nauhoittamalla toiminnon ensin Excelin puolella.

Tyhjien solujen korvaaminen

Seuraava ohjelma korvaa aktiivisen solun ympärillä olevan aineiston tyhjät solut x:llä.

Sub ReplaceEmpty()
    On Error Resume Next
    ActiveCell.CurrentRegion.SpecialCells(xlCellTypeBlanks). _
        Value = "x"
    On Error GoTo 0
End Sub

SpecialCells-menetelmän argumentilla xlCellTypeBlanks löydetään nimen omaan tyhjät solut.

On Error Resume next on tarpeen. Muutoin ohjelma pysähtyy virheeseen, jos tyhjiä soluja ei löydy.

Kaavat arvoiksi

Kaavoilla laskettujen tulosten muuttaminen pelkiksi arvoiksi onnistuu seuraavalla ohjelmalla.

Sub FormulaAsValues1()
    On Error Resume Next
    ActiveCell.CurrentRegion.SpecialCells _
        (xlCellTypeFormulas).Select
    Selection.Copy
    Selection.PasteSpecial Paste:=xlPasteValues
    Application.CutCopyMode = False
    On Error GoTo 0
End Sub

SpecialCells-menetelmän argumentilla xlCellTypeFormulas löydetään nimen omaan tyhjät solut.

Ohjelma heikko kohta on PasteSpecial-menetelmä. Se ei toimi toivotulla tavalla, jos kaavoja sisältävät solut eivät ole vierekkäisissä ja allekkaisissa soluissa. Seuraava ohjelma on parempi, koska se toimii vaikka Select-menetelmän valitsema alue olisi monivalinta.

Sub FormulasAsValues2()
Dim Cell As Range
    On Error Resume Next
    ActiveCell.CurrentRegion.SpecialCells _
        (xlCellTypeFormulas).Select
    For Each Cell In Selection
        Cell.Value = Cell.Value
    Next Cell
    On Error GoTo 0
End Sub

Eri tyyppisten solujen tunnistaminen

Seuraava ohjelma värjää merkkijonotiedon, numerotiedon, kaavat ja tyhjät omilla taustaväreillään

Sub ColorCells()
    On Error Resume Next
    With ActiveCell.CurrentRegion
        .SpecialCells(xlCellTypeConstants, xlNumbers). _
            Interior.Color = RGB(197, 217, 241)
        .SpecialCells(xlCellTypeConstants, xlTextValues). _
            Interior.Color = RGB(242, 220, 219)
        .SpecialCells(xlCellTypeBlanks). _
            Interior.Color = RGB(242, 242, 242)
        .SpecialCells(xlCellTypeFormulas). _
            Interior.Color = RGB(235, 241, 222)
    End With
    On Error GoTo 0
End Sub

Argumentilla xlCellTypeConstants poimitaan solut, jotka eivät sisällä laskentakaavaa. Toisella argumentilla tarkennetaan, onko kyseessä numerotieto xlNumbers vai merkkijonotieto xlTextValues.

Lisätietoa

Lisätietoa Range.SpecialCells -menetelmän argumenteista Range.SpecialCells -menetelmän ohjetoiminnosta.

Tämän artikkelin esimerkit tiedostossa specialcells.xlsm

Autofilter

Tämän artikkelin esimerkit tiedostossa autofilter.xlsm

Yksinkertainen suodatus

Range.Autofilter menetelmällä voit suodattaa aineistosta osa-ainestoja tehokkaasti. Esimerkiksi lause

ActiveCell.AutoFilter Field:=5, Criteria1:=”Korkeakoulu”

suodattaa aktiivisen solun ympärillä olevan aineiston siten että näkyville jäävät vain rivit, joissa on viidennessä sarakkeessa teksti Korkeakoulu.

Seuraavassa ohjelmassa hyödynnän suodattamista. Ohjelma kopioi korkeakoulututkinnon suorittaneiden henkilöiden tiedot uuteen laskentataulukkoon.

Sub MyFilterCopy()
Dim MyRange As Range
Dim NewSheet As Worksheet
    Set MyRange = ActiveCell
    MyRange.AutoFilter Field:=5, Criteria1:="Korkeakoulu"
    Set NewSheet = Worksheets.Add
    MyRange.CurrentRegion.Copy Destination:=NewSheet.Range("A1")
    MyRange.AutoFilter
End Sub

Huomaa erityisesti, että Range-objektin CurrentRegion-ominaisuus tavoittaa suodatetusta aineistota näkyville jääneet rivit. Ohjelman viimeisenä rivinä on AutoFilter-menetelmä ilman argumentteja. Tämä poistaa aineiston suodatukset.

Seuraava ohjelmaa värjää korkeakoulun suorittaneiden rivit vihreiksi.

Sub MyFilterGreen()
Dim MyRange As Range
Dim MyRows As Long
    Set MyRange = ActiveCell
    MyRows = MyRange.CurrentRegion.Rows.Count
    MyRange.AutoFilter Field:=5, Criteria1:="Korkeakoulu"
    MyRange.CurrentRegion.Offset(1).Resize(MyRows - 1) _
        .Interior.Color = RGB(0, 255, 0)
    MyRange.AutoFilter
End Sub

Offset(1).Resize(MyRows-1) tarvitaan, jotta ostsikkoriviä ei värjätä.

Seuraava ohjelma poistaa korkeakoulun suorittaneet aineistosta.

Sub MyFilterRowsDelete()
Dim MyRange As Range
Dim MyRows As Long
    Set MyRange = ActiveCell
    MyRows = MyRange.CurrentRegion.Rows.Count
    MyRange.AutoFilter Field:=5, Criteria1:="Korkeakoulu"
    MyRange.CurrentRegion.Offset(1).Resize(MyRows - 1) _
        .EntireRow.Delete
    MyRange.AutoFilter
End Sub

Voit käyttää Criteria1-argumentin arvoissa jokerimerkkiä *. Esimerkiksi Criteria1:=”*koulu*” jättää näkyville kaikki rivit, joissa esiintyy viidennessä sarakkeessa sana koulu.

Jos haluat hakea tyhjiä soluja, niin käytä Criteria1:=”=”

Jos haluat hakea ei-tyhjiä soluja, niin käytä Criteria1:=”<>”

Operator-argumentti

AutoFilter-menetelmän Operator-argumentin avulla voit tehdä monipuolisempia suodatuksia.

ActiveCell.AutoFilter Field:=7, Criteria1:=”3″, Operator:=xlTop10Items jättää näkyville ne rivit, joissa on seitsemännen sarakkeen kolme suurinta arvoa.

• Field-argumentti määrittää sarakkeen, jota ehto koskee.
• Operator:=xlTop10Items tarkoittaa, että sarakkeesta haetaan suuripia arvoja. On toki hämmentävää, että argumentin arvossa esiintyy luku 10 vaikka välttämättä ei olla hakemassa kymmentä suurinta arvoa.
• Criteria1-argumentin arvolla täsmennetään kuinka monta suurinta haetaan.

Vastaavalla tavalla voit käyttää Operator-argumentin arvoja xlBottom10Items, xlTop10Percent ja xlBottom10Percent. Voit jopa suodattaa värin perusteella käyttämällä argumentin arvoja xlFilterCellColor tai xlFilterFontColor. Värin voi ilmaista RGB-arvona, esimerkiksi Criteria1:=RGB(0,255,0).

Operator-argumentin xlAnd ja xlOr -arvoilla voit yhdistää ehtoja. Esimerkiksi

ActiveCell.AutoFilter Field:=8, Criteria1:=”1″, Operator:=xlOr, Criteria2:=”2″

jättää näkyville ne rivit, joissa on kahdeksannessa sarakkeessa arvo 1 tai arvo 2.

ActiveCell.AutoFilter Field:=7, Criteria1:=”>2000″, Operator:=xlAnd,  Criteria2:=”<3000″

jättää näkyville ne rivit, joissa on seitsemännessä sarakkeessa suurempi kuin 2000, mutta pienempi kuin 3000.

Jos haluat useampia kuin 2 ehtoa, niin voit antaa ehdot vektorina (Array). Tällöin Operator-argumentin arvona on xlFilterValues. Esimerkiksi lause

Range(”A1”).AutoFilter Field:=6, Criteria1:=Array(”1”, ”2”,  ”4”), Operator:=xlFilterValues

jättää näkyville ne rivit, joissa on kuudennessa sarakkeessa arvo 1, 2 tai 4.

Lisätietoa

Lisätietoa Range.AutoFilter -menetelmän ohjetoiminnosta.

Tämän artikkelin esimerkit tiedostossa autofilter.xlsm

Lajittelu eli järjestäminen

Tämän artikkelin esimerkit tiedostossa sort.xlsm

Range.Sort-menetelmä

Range.Sort on suoraviivaisin menetelmä laskentataulukon tietojen lajitteluun.  Sort-menetelmä lajittelee Range-objektin määrittelemän solualueen.

Seuraava ohjelma lajittelee aktiivisen solun ympäriltä löytyvän aineiston käyttäen lajitteluperusteena B-sarakkeen tietoja.

Sub MySort1()
Dim MyRange As Range
    Set MyRange = ActiveCell.CurrentRegion
    MyRange.sort Key1:=Range("B1"), Order1:=xlAscending, _
    Header:=xlYes, MatchCase:=True, Orientation:=xlSortColumns
End Sub

Range.Sort-menetelmän argumentteja

• Key1 määrittää sarakkeen (tai rivin), jonka perusteella lajittelu suoritetaan
• Order1 määrittää onko kyseessä nouseva xlAscending vai laskeva xlDescending järjestys
• Header määrittää onko lajiteltavalla aineistolla otsikot xlYes vai ei xlNo. Jos aineistolla on otsikot, niin on tärkeää käyttää xlYes-arvoa, jotta otsikot pysyvät ensimmäisellä rivillä. Voin myös käyttää xlGuess, jolloin annan Excelin arvata, onko aineistolla otsikot.
• MatchCase määrittää huomioidaanko isojen ja pienten kirjainte ero True vai ei False.
• Orientation määrittää lajitellaanko sarakkeita xlSortColumns vai rivejä xlSortRows.

Muita harvemmin tarvittavia argumentteja löydät Range.Sort-menetelmän ohjetiedoista.

Tarvittaessa voin käyttää jopa kolmea lajitteluperustetta. Seuraavassa on kaksi lajitteluperustetta. Ensisijainen lajittelu suoritetaan B-sarakkeen perusteella nousevaan järjestykseen ja toissijainen lajittelu C-sarakkeen perusteella laskevaan järjestykseen.

Sub MySort2()
Dim MyRange As Range
    Set MyRange = ActiveCell.CurrentRegion
    MyRange.sort Key1:=Range("B1"), Order1:=xlAscending, _
    Key2:=Range("C1"), Order2:=xlDescending, Header:=xlYes, _
    MatchCase:=True, Orientation:=xlSortColumns
End Sub

Sort-objekti

Jos nauhoitat lajittelun, niin nauhoitetussa koodissa käytetään SortObjects-kokoelmaa, SortObject-objektia ja Sort-objektia. Näitä käytettäessä tarvitaan seuraavat vaiheet:

• Laskentataulukon SortFields-kokoelman tyhjentäminen lauseella ActiveSheet.Sort.SortFields.Clear
• Uusien SortField-objektien lisääminen SortFields-kokoelmaan lauseella ActiveSheet.Sort.SortFields.Add
• Sort-objektin Apply-menetelmän käyttö

Seuraava ohjelma lajittelee aktiivisen solun ympäriltä löytyvän aineiston käyttäen ensisijaisena lajitteluperusteena B-sarakkeen tietoja ja toissijaisena lajitteluperusteena E-sarakkeen tietoja.

Sub MySort3()
Dim MyRange As Range
    Set MyRange = ActiveCell.CurrentRegion
    ActiveSheet.sort.SortFields.Clear
    ActiveSheet.sort.SortFields.Add Key:=Range("B1"), _
    SortOn:=xlSortOnValues, Order:=xlAscending
    ActiveSheet.sort.SortFields.Add Key:=Range("E1"), _
    SortOn:=xlSortOnValues, Order:=xlDescending
    With ActiveSheet.sort
        .SetRange MyRange
        .Header = xlYes
        .MatchCase = True
        .Orientation = xlSortColumns
        .Apply
    End With
End Sub

SortField-objektille on tärkeää määrittää Key, SortOn ja Order -ominaisuudet. SortField-objektin avulla voit lajitella jopa värin perusteella, koska SortOn-ominaisuutena voi olla SortOnCellColor tai SortOnFontColor.

Sort-objektille on tärkeää määrittää lajiteltava solualue SetRange-menetelmällä.

Muita SortField-objektin ja Sort-objektin ominaisuuksia löydät ohjetoiminnosta.

Taulukkomuuttujan lajittelu

Taulukkomuuttujan (Array) arvot voit lajitella kirjoittamalla taulukkomuuttujan arvot laskentataulukkoon, jonka jälkeen voit käyttää edellä kuvattuja menetelmiä.

Joissain tilanteissa voi tuntua tarkoituksenmukaisemmalta lajitella taulukkomuuttuja kirjoittamatta sen arvoja laskentataulukkoon. VBA:ssa ei valitettavasti ole valmista menetelmää tätä varten. Tarvitset erillisen funktion, joka suorittaa lajittelun. Pienillä aineistoilla voit käyttää lajitteluun yksinkertaista BubbleSort-lajittelualgoritmia. Excel-tiedostosta sort.xlsm löydät BubbleSort-algoritmia soveltavan funktion, jonka olen kopioinut osoitteesta http://oco-carbon.com/2012/08/13/sorting-functions-for-vba/

Funktiota kutsutaan seuraavan kaltaisella lauseella

MyArray2 = BubbleSort(MyArray1, 2, True)

• MyArray2 on taulukkomuuttuja, johon lajiteltu taulukkomuuttuja sijoitetaan
• MyArray1 on lajiteltava taulukkomuuttuja
• Kolmas argumentti kertoo kuinka monennen taulukkomuuttujan sarakkeen mukaan lajitellaan (esimerkissä 2. sarakkeen mukaan)
• Viimeinen argumentti on True laskevalle järjestykselle ja False nousevalle järjestykselle.

Funktion käytössä täytyy huomioida, että taulukkomuuttujan indeksien oletetaan alkavan arvosta 0. Jos käytät taulukkomuuttujia, joiden indeksit alkavat arvosta 1, niin löydät sovitetun version BubbleSort1 tiedostosta sort.xlsm.

Jos lajiteltavana on tuhansia rivejä, niin BubbleSort on auttamatta liian hidas algoritmi. Tietoa ja keskustelua nopeammista lajittelualgoritmeista löydät netistä esimerkiksi hakusanalla vba sorting algorithms.

MyRandomOrder-ohjelma arpoo nimet satunnaiseen järjestykseen seuraavien vaiheiden kautta:

• Lukee aktiivisen solun ympärillä olevat nimet taulukkomuuttujaan MyArray1
• Arpoo taulukkomuuttujaan satunnaisluvut kunkin nimen viereen
• Lajittelee nimet MyArray2-taulukkomuuttujaan satunnaislukujen mukaiseen järjestykseen BubbleSort1-funktiota käyttäen
• Kirjoittaa taulukkomuuttujan MyArray2 sisällön laskentataulukkoon alkuperäisten nimien viereen.

Sub MyRandomOrder()
Dim MyRange As Range
Dim MyNamesCount As Long
Dim MyArray1() As Variant
Dim MyArray2() As Variant
Dim i As Integer
    Set MyRange = ActiveCell.CurrentRegion
    MyNamesCount = MyRange.Rows.Count
    ReDim MyArray1(1 To MyNamesCount, 1 To 2)
    ReDim MyArray2(1 To MyNamesCount, 1 To 2)
    MyArray1 = MyRange.Resize(, 2)
    For i = 1 To MyNamesCount
        MyArray1(i, 2) = Rnd
    Next i
    MyArray2 = BubbleSort1(MyArray1, 2, True)
    MyRange.Offset(, 2).Resize(, 2) = MyArray1
End Sub

Tämän artikkelin esimerkit tiedostossa sort.xlsm

Python ja Power BI yhteiskäyttö

Päivitetty 15.5.2020

Power BI desktop on hyvä työkalu datojen noutamiseen, yhdistelyyn ja visualisointiin. Visualisoinnit kootaan dashboard-tyyppiselle alustalle ja voidaan edelleen julkaista Power BI -pilvipalvelussa tai omalla Power BI -palvelimella.

Jos visualisointien tekemiseksi tarvitaan edistyneempää data-analytiikkaa, niin apuvälineinä voi käyttää Python- ja R-ohjelmointikieliä. Julkaisualustalle siirrettynä tuettuina ovat ainakin seuraavat Pythonin ohjelmakirjastot: numpy, pandas, matplotlib, seaborn, scikit-learn, scipy ja statsmodels.

Seuraavassa luon Excel-muotoiselle datalle ( http://taanila.fi/data3.xlsx ) jointplotin. Lukijan oletan entuudestaan tuntevan Power BI Desktopin toimintoja ja osaavan jonkin verran Python data-analytiikkaa.

Tässä käytävä esimerkki on yksinkertainen, mutta Python-koodi voisi sisältää paljonkin analytiikkaa kunhan lopputuloksena syntyy visualisointi (matplotlib– tai seaborn-kirjaston kuvio).

Käyttöönotto

Power BI desktopille täytyy kertoa, mitä Python-asennusta käytetään:

• Valitse File – Options and settings – Options.
• Valitse vasemmasta reunasta Python scripting.
• Detected Python home directories -listasta löytyy käyttämästäsi koneesta tunnistetut Python-asennukset, joista voit valita haluamasi. Anacondaa käyttävillä, myös minulla, on ollut ongelmia saada Python toimimaan Power BI:n kanssa. Tähän ongelmaan löytyy erilaisia ratkaisuyrityksiä googlaamalla. Tätä kirjoittaessani poistin koneeltani kaikki Python-asennukset ja asensin Anacondan uusimman version. Tässä tapauksessa Anacondan Python toimi ongelmitta Power BI:ssä.

WinPython on kätevä Windows-koneilla toimiva siirrettävissä oleva paketti, joka ei vaadi minkäänlaista asennusta eikä myöskään vaikuta mitenkään koneella jo oleviin Python asennuksiin. Tätä voit käyttää PowerBI:n kanssa, jos et saa muita asennuksia yhteistyöhön. PowerBI ei automaattisesti tunnista koneella olevaa WinPythonia, mutta sen voi ottaa käyttöön valitsemalla Detected Python home directories -listasta Other ja siirtymällä Browse-toiminnolla WinPythonin kansioon:

Visualisointi Pythonilla

Napsauta Visualizations-paneelissa Py-kuvaketta.

Jos saat pyynnön sallia visualisoinnit, niin valitse Enable.

Alareunaan ilmestyy Python script editor, jossa on teksti Drag fields into Values area in the Visualization pane to start scripting. Toimi ohjeen mukaan ja lisää tarvitsemasi kentät Value-alueelle.

Power BI muodostaa valituista kentistä pandas dataframen, jonka nimenä on dataset.

Tärkeää: Power BI poistaa duplikaatit eli rivit, joilla on täsmälleen samat arvot. Jos haluat säilyttää kaikki rivit, niin lisää Value-alueelle myös kenttä, jossa jokaisella rivillä on eri arvo (tässä esimerkissä nro).

Python script editor on valmiina koodia varten. Lisättävän koodin toimivuus kannattaa ehdottomasti testata ohjelmointiympäristössä, jossa yleensä koodaat. Virheiden metsästäminen ja korjaaminen on Power BI:ssä työlästä.

Seuraavassa olen kopioinut koodin Python script editoriin:

Koodin voi suortittaa editorin oikean yläkulman Run script -painikkeella:

Yllä näkyvästä olen lisäksi poistanut Power BI:n tuottaman otsikon.

Ongelmia desimaalipilkkujen kanssa

Pythonia voi käyttää datan noutamiseen valitsemalla Get data – Other – Python script – Connect. Tämän jälkeen pääset kirjoittamaan koodin datan avaamiseen:

Tämä kuitenkin johtaa ongelmiin Suomessa:

• Python käyttää aina desimaalierottimena pistettä.
• PowerBI puolestaan tunnistaa pisteitä sisältävän tiedon päivämäärätyyppiseksi.

Seurauksen huomaa tietoa noudettaessa:

Tästä voi toki jatkaa Power Query Editoriin, jossa voi kumota päivämääräksi muuntamisen, korvata pisteet pilkuilla ja antaa sen jälkeen Power BI:n tunnistaa tietotyyppi. Useimmissa tapauksissa kannattanee kuitenkin välttää datan avaamista Python scriptillä.

Power Query Editorissa voit halutessasi muuntaa ja siivota dataa Python scripteillä. Run Python Script -painike löytyy Transform-välilehdeltä.

Toisaalta Power Query Editor tarjoaa monipuoliset toiminnot datan muuntamiseen ja siivoamiseen ilman Python scriptejäkin.

Lisätietoa

https://docs.microsoft.com/fi-fi/power-bi/connect-data/desktop-python-visuals

 

 

 

 

 

Lukumäärä- ja prosenttiyhteenvedot Pythonilla

Päivitetty 8.2.2024

Lukumäärä- ja prosenttiyhteenvedot tulevat kyseeseen seuraavissa tapauksissa:

• Kategorisen muuttujan yhteenvetotaulukko (frekvenssitaulukko) tai frekvenssien esittäminen pylväskaaviona.
• Määrällisen muuttujan luokiteltu jakauma frekvenssitaulukkona tai histogrammina.
• Dummy-muuttujien (dikotomisten muuttujien) yhteenveto. Dummy-muuttujaksi kutsutaan muuttujaa, joka saa arvokseen joko 0 (joskus tämän sijasta käytetään tyhjää) tai 1. Esimerkiksi kyselytutkimuksessa monivalintakysymys, jonka vaihtoehdoista vastaaja saa valita useammankin kuin yhden, koodataan dummy-muuttujiksi: Jokainen kysymyksen vaihtoehto on muuttuja, joka saa arvokseen 1, jos vastaaja on sen valinnut. Muussa tapauksessa arvo on 0 tai tyhjä.
• Kategoristen muuttujien välisen riippuvuuden tarkastelu ristiintaulukoimalla.

Frekvenssitaulukko

Frekvenssitaulukon lasken pandas-kirjaston crosstab-funktiolla.

Jos kategoristen muuttujien arvot eivät ole tekstimuodossa, niin määrittelen numeroiden tekstimuotoiset vastineet listoina. Listan voin sijoittaa taulukon indeksin arvoksi.

Voin visualisoida lukumääriä tai prosentteja vaaka- tai pystypylväskaaviona. Yhteensä-rivin tietoja en esitä pylväänä. Jos esitän kaaviossa prosentteja, niin näytän n-arvon (lukumäärä, josta prosentit on laskettu; esimerkiksi edellisessä taulukossa n=81).

Tarkemmat yksityiskohdat selviävät esimerkistä.

Luokiteltu jakauma

Määrällisen muuttujan jakaumaan tutustun luokitellun jakauman avulla.

Pythonilla on helppo kokeilla erilaisia luokkien lukumääriä tai luokkarajoja tilanteeseen sopivan luokittelun löytämiseksi. Olen tottunut käyttämään luokitteluun kahta menetelmää:

• Pandas kirjaston cut-funktiolla voin lisätä luokat alkuperäiseen dataan ja laatia sen jälkeen frekvenssitaulukon crosstab-funktiolla.
• Mieluummin laadin histogrammin suoraan datasta seaborn kirjaston histplot-kaaviolajia käyttäen.

Tarkemmat yksityiskohdat selviävät esimerkistä.

Dummy-muuttujien yhteenveto

Yhteenvetoon mukaan otettavat muuttujat määrittelen listana. Tämän jälkeen lasken listan mukaisista muuttujista lukumäärät:

• Jos dummy-muuttujan arvoina on ykkösiä (ja nollia tai tyhjiä) niin käytän sum-funktiota.
• Jos dummy-muuttujan arvoina on ykkösten sijasta joitain muita numeroita ja tyhjiä niin käytän count-funktiota (laskee lukujen lukumäärän).

Tärkeää: Prosentit lasken kaikista vastaajista (=koko otoksesta). Taulukon yhteydessä täytyy ilmoittaa n-arvo (edellä n=82).

Tarkemmat yksityiskohdat selviävät esimerkistä.

Ristiintaulukointi

Kahden kategorisen muuttujan välinen riippuvuus selviää ristiintaulukoimalla. Laadin ristiintaulukoinnin crosstab-funktiolla.

Tärkeää: Jos selittävän muuttujan arvot ovat sarakkeissa, niin käytän prosentteja sarakkeen kokonaismäärästä (columns). Jos selittävän muuttujan arvot ovat riveillä, niin käytän prosentteja rivin kokonaismäärästä (index).

Tärkeää: Jos käytän prosentteja niin minun on kerrottava mistä lukumääristä prosentit on laskettu (n-arvot). Edellä prosentit on laskettu naisten kohdalla naisten lukumäärästä (n=19) ja miesten kohdalla miesten lukumäärästä (n=62).

Jos otoksesta lasketussa ristiintaulukoinnissa on havaittavaa riippuvuutta, niin voin tarkistaa khiin neliö -testillä, onko riippuvuus tilastollisesti merkitsevää?

Tarkemmat yksityiskohdat selviävät esimerkistä.

value_counts()

Frekvenssitaulukot ja ristiintaulukoinnit voin siis laskea crosstab()-funktiolla, mutta taitavalle käyttäjälle value_counts() on kätevämpi ja antaa enemmän mahdollisuuksia.

Tarkemmat yksityiskohdat selviävät esimerkistä.

Koneoppimisen käsitteitä

Päivitetty 25.8.2022

Data-analytiikan tasot

Data-analytiikka voidaan jakaa neljään tasoon seuraavasti:

Kuvailevassa analytiikassa esitetään muuttujien jakaumia frekvenssitaulukoina ja tilastollisina tunnuslukuina. Selittävässä analytiikassa tarkastellaan muuttujien välisiä riippuvuuksia ristiintaulukoimalla, tunnuslukujen vertailulla ja korrelaatioilla. Ennakoivaan analytiikkaan käytetään koneoppimisen malleja. Ohjaava analytiikka perustuu kuvailevaan, selittävään ja ennakoivaan analytiikkaan, mutta voi sisältää myös muunlaisia laskentamenetelmiä, esimerkiksi lineaarista optimointia.

Koneoppimisen menetelmien jaottelu

Ennakoivaan analytiikkaan käytettävät koneoppimisalgoritmit voidaan luokitella  seuraavasti:

• Ohjattu oppiminen (supervised learning): Algoritmi opetetaan opetusdatalla (training data). Esimerkiksi roskapostisuodatin opetetaan sähköpostidatalla, jossa on erilaisia tietoja kustakin sähköpostiviestistä sekä tieto siitä oliko sähköpostiviesti roskapostia. Tämän datan perusteella muodostuu malli, jota käyttäen tulevista sähköpostiviesteistä voidaan tunnistaa roskapostiviestejä.
• Ohjaamaton oppiminen (unsupervised learning): Esimerkiksi asiakkaiden jakaminen asiakkaiden tietoja sisältävän datan perusteella asiakassegmentteihin.
• Vahvistusoppiminen (reinforcement learning): Algoritmi suorittaa toimia ja saa niistä palautetta palkkioiden ja rangaistuksen muodoissa. Algoritmi oppii saamistaan palkkioista ja rangaistuksista. Vahvistettua oppimista käytetään esimerkiksi robotiikassa.

Seuraavassa jaotellaan ohjattu ja ohjaamaton oppiminen edelleen alatyyppeihin:

Ohjattu oppiminen

Ohjatussa oppimisessa:

• Algoritmi muodostaa (oppii) mallin opetusdatan (training set) avulla.
• Opetusdata koostuu selittävien muuttujien arvoista (feature matrix) ja  kohdemuuttujan arvoista (labels).
• Opetusdatassa kohdemuuttujan arvot ovat tiedossa!
• Opetettu malli osaa ennustaa kohdemuuttujan arvoja uudelle datalle.

Ohjatun oppisen prosessi etenee seuraavan kaavion mukaisesti:

Ohjattua oppimista, jossa kohdemuuttuja on kategorinen käytetään esimerkiksi seuraavissa:

• Roskapostisuodatin
• Sairauden diagnosointi
• Maksuhäiriön ennakointi
• Vakuutuspetoksen tunnistaminen
• Auton rekisterinumeron koneellinen lukeminen
• Esineiden tunnistaminen valokuvasta

Tällaisissa tilanteissa kyse on luokittelusta (classification). Suosittuja luokittelumalleja ovat esimerkiksi:

• Logistinen regressio
• Päätöspuu (decision tree)
• Satunnaismetsä (random forest)
• Gradienttitehostus (gradient boosting)

Käytännössä lineaarisesti erotettavissa olevat luokat ovat helpompia erotella:

Ohjattua oppimista, jossa kohdemuuttuja on määrällinen käytetään esimerkiksi seuraavissa:

• Kysynnän ennustaminen
• Asunnon myyntihinnan ennustaminen
• Käytetyn auton myyntihinnan ennustaminen

Tällaisissa tilanteissa käytetään erilaisia regressiomalleja. Suosittuja malleja ovat esimerkiksi

• lineaarinen regressio
• satunnaismetsä regressio (random forest regressor)
• gradienttitehostus regressio (gradient boosting regressor)

Ohjaamaton oppiminen

Ohjaamatonta oppimista voidaan käyttää esimerkiksi asiakassegmenttien muodostamiseen. Ohjaamattomassa oppimisessa on käytössä ainoastaan selittävät muuttujat (feature matrix).

Käytetyin menetelmä on K-means klusterointi, missä K viittaa muodostettavien klusterien lukumäärään, joka tässä menetelmässä päätetään etukäteen.

Datan yksinkertaistamiseen, havainnollistamiseen ja taustalla olevien rakenteiden tunnistamiseen voidaan käyttää pääkomponenttianalyysia (Principal component analysis). Tällä menetelmällä selittävistä muuttujista muodostetaan laskennallisesti pienempi joukko muuttujia.  Seuraavissa kuvioissa on pelkistetty alkuperäinen kolmen muuttujan asetelma kahden muuttujan asetelmaksi.

Pääkomponenttianalyysillä voidaan esimerkiksi eri oppiaineissa menestymisen takaa tunnistaa erilaisia lahjakkuuksia (verbaalinen, matemaattinen jne.).

Neuroverkot

Edellä kuvattuja menetelmiä käytetään etupäässä strukturoidun datan (taulukkomuotoinen data) kanssa. Koneoppimista hyödynnetään myös strukturoimattoman datan kanssa. Strukturoimatonta dataa ovat esimerkiksi tekstit, äänet, kuvat ja videot. Neuroverkkomallit ovat käytännössä osoittautuneet käyttökelpoisiksi strukturoimattoman datan tapauksessa. Neuroverkkomalleja voidaan käyttää esimerkiksi:

• Käsinkirjoitetun tekstin tunnistamiseen
• Puheen tunnistamiseen
• Kielen kääntämiseen
• Positiivisten ja negatiivisten viestien tunnistamiseen keskustelualueilta
• Esineiden ja henkilöiden tunnistamiseen kuvista tai videoista
• Konenäköön

Neuroverkkoihin liittyvää koneoppimista kutsutaan syväoppimiseksi (deep learning).

Koneoppiminen ja scikit-learn -kirjasto

Päivitetty 21.9.2022

Pythonia käytettäessä useimmat koneoppimisen mallit löytyvät sklearn (scikit-learn) -kirjastosta. Tästä artikkelista opit  sklearn-kirjaston mallien käytön perusperiaatteet.

Mallien käyttö sujuu seuraavien vaiheiden kautta:

• Valmistele data
• Tuo malli
• Sovita malli dataan
• Arvioi mallin sopivuutta dataan
• Ennusta mallin avulla

Valmistele data

Käytettävään dataan täytyy tutustua huolellisesti etukäteen. Erityisesti kannattaa kiinnittää huomiota seuraaviin:

• Puuttuvat arvot: Useimmat mallit eivät siedä puuttuvia muuttujien arvoja. Puuttuvia arvoja sisältävät rivit pitää joka poistaa tai korvata puuttuvat arvot tarkoituksenmukaisella tavalla.
• Kategoriset muuttujat: Useimmat mallit edellyttävät muuttujien olevan määrällisiä. Kategorisia muuttujia voidaan käyttää, jos ne puretaan dikotomisiksi muuttujiksi eli dummy-muuttujiksi (katso https://www.fsd.tuni.fi/fi/palvelut/menetelmaopetus/kvanti/mittaaminen/ominaisuudet/).
• Skaalaus: Jos selittävät muuttujat poikkeavat suuruusluokaltaan toisistaan, niin yleensä muuttujat kannattaa skaalata samaan suuruusluokkaan. Tämän voi tehdä esimerkiksi muuntamalla muuttujan arvot standardipisteiksi (muuttujan arvosta vähennetään keskiarvo ja erotus jaetaan keskihajonnalla eli lasketaan kuinka monen keskihajonnan päässä keskiarvosta ollaan).

Ohjatun (supervised) oppimisen malleissa tarvitset kaksi dataframea:

• Selittävien muuttujien arvot (feature-matriisi , x-muuttujat). Selittävien muuttujien dataframen nimeksi voit antaa esimerkiksi X.
• Kohdemuuttujan arvot (target, labels, y-muuttuja). Kohdemuuttujan dataframen nimeksi voit antaa esimerksi y.

Tuo malli

Tuo malli sklearn-kirjastosta. Esimerkiksi lineaarisen regressiomallin tuot seuraavasti:

from sklearn.linear_model import LinearRegression

Sovita malli dataan

Sovita malli dataan fit-funktiolla ja tallenna syntyvä olio muuttujan arvoksi. Esimerkiksi seuraavassa sovitetaan lineaarinen regressio dataan X (selittävien muuttujien dataframe) ja y (ennustettavan muuttujan arvot).

malli = LinearRegression().fit(X, y)

Syntynyt olio (malli)  sisältää monenlaista tietoa mallista. Monissa netistä ja kirjallisuudesta löytyvissä esimerkeissä edellinen tehdään kahdessa vaiheessa:

malli = LinearRegression()
malli.fit(X, y)

Tuloksena syntynyt malli-olio on sama muodostettiinpa se kummalla tavalla tahansa.
Mallia voidaan tuunata niin kutsutuilla hyperparametreilla. Esimerkiksi seuraavassa muodostetaan lineaarinen regressiomalli, johon ei otetan mukaan lainkaan vakiotermiä (intercept).

malli = LinearRegression(fit_intercept = False).fit(X, y)

Mallien tuunaus hyperparametreilla edellyttää mallien hyvää tuntemusta.

Arvioi mallin sopivuutta

Sopivuuden arviointiin on monia menetelmiä. Regressiomalleille voit esimerkiksi tulostaa selityskertoimen arvon komennolla malli.score(X, y). Selityskerroin ilmoittaa kuinka monta prosenttia selitettävän muuttujan vaihtelusta malli selittää.

Ennusta mallin avulla

Ennakoivassa analytiikassa keskeisin vaihe on tietenkin ennusteiden laskeminen uudelle datalle. Jos dataframe X_uusi sisältää uusia selittävän muuttujan arvoja, niin saat ennusteet komennolla:

malli.predict(X_uusi)

Lisätietoa

Lisätietoa koneoppimisen koodiesimerkeistä https://tilastoapu.wordpress.com/python/

Miksi Python?

Päivitetty 6.2.2024

Miksi vaivautua koodaamaan, koska datojen analysointiin sopivia valmisohjelmia (Excel, SPSS jne.) on olemassa? Seuraavassa muutamia Pythonin vahvuuksia:

• Python kattaa kaikki data-analytiikan osa-alueet.
• Jos sinulla ei ole aiempaa kokemusta koodauksesta, niin opit samalla koodaamaan yhdellä suosituimmista ohjelmointikielistä.
• Python on ketterä ja toimii hyvin isojenkin datojen kanssa.
• Perusasiat hoituvat helposti. Esimerkiksi komennolla data.describe() saat datan kaikkien muuttujien keskeisimmät tilastolliset tunnusluvut ja komennolla data.corr() saat datan muuttujien väliset korrelaatiot.
• Kerran kirjoitettu koodi on aina suoritettavissa uudelleen. Voit analysoida rakenteeltaan samanlaisia datoja ilman koodin uudelleen kirjoittamista. Voit pienin muutoksin hyödyntää kerran kirjoitettua koodia uusien datojen kanssa.
• Koodi toimii dokumentaationa tehdyistä analyyseistä. Voit milloin tahansa tehdä muutoksia koodiin ja suorittaa analyysit uudelleen.
• Python tarjoaa monipuoliset mahdollisuudet tulosten graafiseen havainnollistamiseen.
• Python on yleiskäyttöinen ohjelmointikieli ja sillä laskettuja tuloksia voit käyttää syötteenä muille ohjelmille.
• Pythonilla voit automatisoida data-analytiikkaa.
• Ohjemateriaalia ja esimerkkejä löytyy helposti netistä. Jos kohtaat ongelman, niin kirjoittamalla Googleen englanninkielisen kysymyksen löydät yleensä myös vastauksen (usein stackoverflow-sivustolta). Myös tekoäly (ChatGPT, Bard, Amazon Q jne.) osaa auttaa.
• Python toimii samalla tavoin Windows-, Linux– ja MacOS-käyttöjärjestelmissä.
• Python on ilmainen.
• Pythonilla voit ohjelmoida ja automatisoida myös Exceliä.

Kuviot ja kaaviot Pythonilla

Päivitetty 10.12.2023

Tehdään aluksi selväksi kuvion (figure) ja kaavion (axes) ero. Kuviota voit ajatella kehykseksi, jonka sisällä on yksi tai useampia kaavioita. Kuvion ja kaavion suhdetta toisiinsa kuvaa oheinen osoitteesta https://realpython.com/python-matplotlib-guide/ lainattu havainnollistus:

Kaavion laadinnassa ja muotoilussa päähuomio kiinnittyy kaavioon eli Axes-luokan olioon ja sen sisältämiin olioihin. Kuvioon eli Figure-luokan olioon huomio kiinnittyy esimerkiksi kuvion koon määrittelyssä, usean kaavion kuvioita laadittaessa ja kuviota tallennettaessa.

Kuvioiden ja kaavioiden peruskirjasto on matplotlib.pyplot. Sen lisäksi kannattaa opetella käyttämään matplotlibin varaan rakennettua seaborn-kirjastoa. Näiden kirjastojen tuonti sujuu seuraavasti:

import matplotlib.pyplot as plt
import seaborn as sns

Jos kaaviot eivät tulostu näkyviin Jupyter notebookissa, niin lisää kirjastojen tuonnin jälkeen komento %matplotlib inline (yleensä tätä ei tarvita).

Matplotlib

Pandas-kirjastossa on oma helppokäyttöinen käyttöliittymä matplotlib-grafiikkaan. Voin luoda kaavion suoraan dataframesta tai dataframen sarakkeesta. Esimerkiksi pystypylväskaavion (bar) voin luoda:

df.plot(kind='bar')

Muita usein käytettyjä kaaviolajeja ovat ’barh’ (vaakapylväs), ’pie’ (piirakka) ja ’line’ (viiva). Viivakaavio on oletuksena, jos kaaviolajin nimi jätetään pois ( df.plot() )

Kaavion luonnin yhteydessä voin tehdä kaavioon liittyviä asetuksia parametreilla, esimerkiksi:

• figsize arvoksi voin asettaa kuvion leveyden ja korkeuden, esimerkiksi (6, 4)
• legend arvoksi voin asettaa False tai ’reverse’. Oletusarvona on True. legend=’reverse’ kääntää selitteen arvojen järjestyksen.
• width arvoksi voin asettaa luvun väliltä 0 – 1. Oletusarvona on 0.5. Mitä suurempi arvo, sitä lähempänä toisiaan ja sitä paksumpia pylväät ovat. Jos width=1, niin pylväät ovat kiinni toisissaan.
• rot kääntää luokka-akselin jakoviivojen (ticks) nimiöt annetun asteluvun mukaan. Esimerkiksi rot=45 kääntää nimiöt 45 asteen kulmaan.
• stacked=True luo pinotun pylväskaavion.
• color määrittää pylväiden värin. Esimerkiksi color=’C0′ asettaa väriksi käytössä olevan väripaletin ensimmäisen värin. Voin käyttää värien nimiä tai koodeja.
• style määrittää viivakaavion viivan ja havaintopisteiden tyylin. Esimerkiksi style=’ro-’ tekee punaisen (r) viivan (–), jossa havaintopisteet ovat ympyröitä (o). Lisätietoa https://matplotlib.org/stable/api/_as_gen/matplotlib.axes.Axes.plot.html
• edgecolor määrittää pylväiden reunan värin.

Lisätietoa ominaisuuksista, jotka voit asettaa parametreilla:

https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.plot.html

Parametrien lisäksi voin muotoilla kaaviota matplotlib.pyplot-funktioilla. Esimerkiksi kaavion otsikon voin lisätä komennolla plt.title(’Kaavion otsikko’). Funktiot kohdistuvat aina viimeksi luotuun kaavioon. Lisätietoa:

https://matplotlib.org/stable/api/pyplot_summary.html

Jos tarvitsen muotoiluja, joita en pääse tekemään plt-funktioilla, niin sijoitan kaavion muuttujan arvoksi, jotta voin viitata kaavioon myöhemmin.

ax = df.plot.bar()

Jos aion viitata myöhemmin myös kuvioon (figure), niin voin ennen kaavion määrittelyä luoda ”tyhjän kuvion ja kaavion” plt.subplots-funktiolla. plt.subplots() palauttaa sekä kuvion (jolle seuraavassa annettu nimi fig) että kaavion (jolle seuraavassa annettu nimi ax). Kaavion laadinnassa ilmoitan ax-parametrin arvona kaavion nimen:

fig, ax = plt.subplots()
df.plot(kind='bar', ax = ax)

Vaihtoehtoisesti voin viitata kuvioon ja kaavioon käyttämällä funktioita plt.gcf() (get current figure) ja plt.gca() (get current axes).

Seaborn

Jos teen kaavioita lasketuista yhteenvetotaulukoista (frekvenssitaulukko, ristiintaulukointi jne.), niin käytän edellä kuvattuja tapoja. Jos taas teen kaavion suoraan datasta, niin käytän yleensä seaborn-kirjaston kaaviolajeja. Seaborn-kaavioita voin muotoilla tavallisten matplotlib-kaavioiden tapaan plt-funktioilla. Myös monet kaavion luonnin matplotlib-parametrit ovat käytettävissä.

Seaborn-kaavion luontitoiminnossa figsize-parametri ei ole käytössä. Jos kuvion koko halutaan määrittää, niin se pitää tehdä luomalla kuvio ennen seaborn-kaavion laadintaa. Seuraava esimerkki kuvaa määrätyn kokoisen countplot-kaavion laatimista tips-nimisen dataframen size-nimisestä muuttujasta.

plt.figure(figsize=(6, 4))
sns.countplot(x='size', data=tips)

Seaborn-kaavioita on mukava laatia kunhan pääset sinuiksi käytetyimpien parametrien kanssa:

• data (dataframe)
• x (x-akselin muuttuja)
• y (y-akselin muuttuja)
• hue (minkä muuttujan mukaan värierottelu)

Seuraavaksi

Pääset hyvään alkuun käymällä läpi kahdeksan muistion sarjan. Aloita tästä:

https://nbviewer.jupyter.org/github/taanila/kaaviot/blob/master/matplotlib1.ipynb

Voit myös aloittaa suoraan seaborn-kaavioista:

https://nbviewer.org/github/taanila/kaaviot/blob/master/seaborn.ipynb

Jupyter: Taulukot ja kaaviot raporttiin

Päivitetty 1.7.2019.

Tässä artikkelissa kerron, miten voit siirtää Pythonilla Jupyter-notebookiin lasketut taulukot ja kaaviot Word-raporttiin.

Taulukot

Jupyter-notebook toimii oletusselaimessa. Laskettujen (html-muotoisten) taulukoiden ulkoasu riippuu käytetystä selaimesta.

Ennen Wordiin kopiointia taulukon lukumuotoilut kannattaa laittaa kuntoon (desimaalien määrä, mahdolliset prosenttimuotoilut).

Valitse taulukko ja kopioi-liitä se Word-dokumenttiin. Näin saat Word-taulukon, jonka ulkoasua voit  muuttaa Wordin taulukkotyökaluilla:

• Valitse solu taulukon alueelta.
• Valitse Table Tools – Design -työkaluista haluamasi tyyli.

Vieressä on kuvakaappaus Jupyter-notebookista.

Kopioi-liitä liittää sen Wordiin karun näköisenä taulukkona (keskimmäinen taulukko).

Tämän jälkeen valitsin Table Tools – Design (Taulukkotyökalut – Rakenne) -työkaluista mieleiseni tyylin. Tästä voisin vielä jatkaa esimerkiksi tasaamalla koulutuksia kuvaavat tekstit vasempaan reunaan, korvaamalla desimaalipisteet pilkuilla ja vaihtamalla fonttia.

Taulukon sisältöä, tekstejä ja lukuja, voin tarvittaessa muokata.

Kaaviot

Samassa Jupyter-notebookin solussa luodun kaavion voit tallentaa komennolla

plt.savefig('nimi.png', bbox_inches='tight')

Tärkeitä huomioita:

• Jos tiedostonimeen ei liity polkua, niin kaavio tallentuu samaan kansioon kuin Jypyter-notebook.
• Ilman bbox_inches=’tight’-parametria kaavion reunoilla olevat tekstit jäävät usein osittain tallennetun kaavion ulkopuolelle.
• Tiedostoformaatti määräytyy tiedostonimen tarkentimesta (edellä .png).

Järjestelmäsi tukemat kuvaformaatit saat selville komennolla

plt.figure().canvas.get_supported_filetypes()

Tuloksena saat listauksen kuvaformaateista, esimerkiksi:

{'ps': 'Postscript',
 'eps': 'Encapsulated Postscript',
 'pdf': 'Portable Document Format',
 'pgf': 'PGF code for LaTeX',
 'png': 'Portable Network Graphics',
 'raw': 'Raw RGBA bitmap',
 'rgba': 'Raw RGBA bitmap',
 'svg': 'Scalable Vector Graphics',
 'svgz': 'Scalable Vector Graphics',
 'jpg': 'Joint Photographic Experts Group',
 'jpeg': 'Joint Photographic Experts Group',
 'tif': 'Tagged Image File Format',
 'tiff': 'Tagged Image File Format'}

Kaavion voit myös kopioida Jupyter-notebookista suoraan Wordiin kopioi-liitä-toiminnolla (löydät kopioi-komennon napsauttamalla hiiren kakkospainiketta kaavion päällä).

Kaavioiden fontti

Kaavion  fonttia et voi vaihtaa enää raportissa. Pythonilla fontin vaihto onnistuu, mutta se pitää tehdä ennen kaavioiden luontia. Voit antaa seuraavat komennot heti ohjelmakirjaston tuonnin (import  matplotlib.pyplot as plt) jälkeen. Komennot vaikuttavat näin kaikkiin samassa notebookissa laadittaviin kaavioihin.

plt.rcParams['font.sans-serif'] = "Arial"
plt.rcParams['font.family'] = "sans-serif"

Ensimmäisellä komennolla määrität fonttilajin. Yllä on määritelty ’sans-serif’-fontiksi ’Arial’. Sen jälkeen on määritelty, että kaavioissa käytetään ’sans-serif’-fonttia. ’sans-serif’ tarkoittaa fontteja ilman pääteviivaa (groteski). Voit myös määrittää käytettäväksi ’serif’-fontin eli pääteviivallisen fontin.

Voit halutessasi säätää myös fonttikoot, esimerkiksi:

plt.rcParams['font.size'] = 12 #oletusfontti
plt.rcParams['axes.titlesize'] = 14 #kaavion otsikko
plt.rcParams['axes.labelsize'] = 12 #akselien otsikot
plt.rcParams['xtick.labelsize'] = 10 #x-akselin jaotuksen nimiöt
plt.rcParams['ytick.labelsize'] = 10 #y-akselin jaotuksen nimiöt
plt.rcParams['legend.fontsize'] = 12 #selite
plt.rcParams['figure.titlesize'] = 14 #kuvion otsikko

 

Github – esimerkit omalle koneelle

Päivitetty 6.2.2024

Olen tallentanut esimerkkikoodeja Jypyter-muistioina githubiin. Esimerkit aukeavat selaimeen, josta voit halutessasi kopioida koodin pätkiä (solu kerrallaan) itsellesi. Kokonaisen Jupyter-muistion tallentaminen omalle koneelle Jupyter-muistiona ei välttämättä onnistu, mutta voit kloonata kokonaisen kansion omalle koneellesi:

• Siirry osoitteeseen https://github.com/taanila
• Valitse repository (kansio), jonka haluat kloonata (kaaviot, data, kuvaileva, selittava, aikasarjat, jne.)
• Napsauta vihreää Code-painiketta ja valitse Download ZIP
• Pura (Extract all) tallentamasi paketti omaan kotikansioosi (sinne, missä säilytät Python-koodejasi). Paketti purkautuu omaan kansioonsa (esimerkiksi kaaviot-master).

Kaikki esimerkit ovat tämän jälkeen avattavissa Jupyteriin.

Päivitän esimerkkejä aika ajoin. Tuoreimmat versiot saat käyttöösi suorittamalla yllä kuvatun kloonauksen uudelleen.

Lineaarinen regressio 3

Jos koneoppiminen ja sklearn (scikit-learn) -kirjasto ovat sinulle täysin uusia, niin lue ennen tätä artikkelia Lineaarinen regressio 1 ja Lineaarinen regressio 2.

Tämän artikkelin ohjelmakoodin ja tulosteet löydät GitHubista:

https://github.com/taanila/tilastoapu/blob/master/linreg3.ipynb

Jos kopioit koodia itsellesi, niin kannattaa käyttää GitHubia. Tästä artikkelista kopioidut koodit eivät välttämättä toimi oikein.

Tämän artikkelin esimerkkidatana käytän sklearn kirjastosta löytyvää dataa Bostonin asuntojen hinnoista. Artikkelin ideat olen lainannut osoitteesta

https://towardsdatascience.com/linear-regression-on-boston-housing-dataset-f409b7e4a155

Ohjelmakirjastojen tuonti

Kuvailevasta analyysistä tutut peruskirjastot ovat tarpeen:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

Datan valmistelu

Lataan esimerkkiaineiston sklearn-kirjastosta seuraavasti:

from sklearn.datasets import load_boston
boston_data = load_boston()

Aineistossa on eroteltu data (features), target (selitettävä muuttuja), feature_names (selittävien muuttujien nimet) ja DESCR (aineiston kuvaus). Tämä selviää keys()-funktiolla:

print(boston_data.keys())

dict_keys([’data’, ’target’, ’feature_names’, ’DESCR’])

Komennolla print(boston_data.DESCR) voit lukea aineiston kuvauksen.

Luon aineiston perusteella boston-nimisen dataframen:

boston = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
boston['MEDV'] = boston_data.target
boston.head()

Selitettävä muuttuja MEDV kuvaa asuntojen mediaanihintoja tuhansina dollareina eri alueilla. Muut muuttujat ovat ehdokkaita mediaanihintaa selittäviksi muuttujiksi (voit lukea lisää aineiston kuvauksesta).

Varmuuden vuoksi kannattaa tarkistaa, onko datassa puuttuvia arvoja:

boston.isnull().sum()

Puuttuvia arvoja ei ole, mikä on hyvä asia.

Seuraavaksi katson miten selitettävän muuttujan MEDV arvot ovat jakautuneet. Käytän tarkasteluun seaborn-kirjaston distplot-kuviota ja luokittelen hinnat 30 luokkaan:

sns.distplot(boston['MEDV'], bins=30)

Kuvion mukaan asuntojen mediaanihintojen jakauma on oikealle vino. Vinoudesta huolimatta yritetään mallintaa hintoja lineaarisella regressiolla.

Selittävien muuttujien valinnassa voin hyödyntää korrelaatiokertoimia. Seaborn-kirjaston heatmap-funktiolla voin värjätä corr()-funktiolla lasketut korrelaatiokertoimet niiden arvon mukaan. Oletusarvolla heatmap tulostaa vain värilliset ruudut, mutta lisäparametrilla annot=True saan myös korrelaatiokertoimien arvot näkyviin:

correlation_matrix = boston.corr().round(2)
plt.figure(figsize=(12,9))
sns.heatmap(data=correlation_matrix, annot=True)

Kaikkein eniten MEDV-muuttujan kanssa korreloivat RM (0,7) ja LSTAT (-0,74). Katson vielä kuvion avulla miltä kyseisten muuttujien korrelaatio MEDV-muuttujan kanssa näyttää. Seuraava koodi toimii vaikka lisäisit enemmänkin muuttujia features-listaan:

features = ['LSTAT', 'RM']
target = boston['MEDV']
plt.figure(figsize=(10, 5))
for i, col in enumerate(features):
   plt.subplot(1, len(features) , i+1)
   plt.scatter(boston[col], target)
   plt.xlabel(col)
   plt.ylabel('MEDV')

Riippuvuus on selkeää molemmissa tapauksissa, mutta erityisesti LSTAT-muuttujan kohdalla riippuvuus ei ole täysin suoraviivaista. Tästä huolimatta jatketaan eteenpäin.

Valmistellaan vielä X (features-matriisi) ja y (target) mallintamista varten:

X = boston[['LSTAT', 'RM']]
y = boston['MEDV']

Opetusdata ja testidata

Jos dataa on riittävästi, niin kannattaa jakaa se opetusdataan ja testidataan. Testidatan avulla voidaan arvioida opetusdatan perusteella laadittua mallia. Seuraavassa jaan datan sattumanvaraisesti opetusdataan ja testidataan (20 % datasta). Parametri random_state asettaa satunnaislukugeneraattorin siemenluvun. Jos jätän sen asettamatta, niin saan eri kerroilla erilaisen jaon opetusdataan ja testidataan. Käyttämällä samaa siemenarvoa saan aina saman jaon.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, 
   test_size = 0.2, random_state=5)
print(X_train.shape)
print(X_test.shape)

(404, 2)
(102, 2)

Huomaan, että opetusdatassa on 404 havaintoa ja testidatassa 102 havaintoa.

Mallin sovitus

Mallin sovitukseen kuuluu LinearRegression-mallin tuonti lineaaristen mallien kirjastosta ja mallin sovitus fit-funktiolla.

from sklearn.linear_model import LinearRegression
malli = LinearRegression()
malli.fit(X_train, y_train)

Tuloksesta näen  mallin lähtötiedot, joita olisin halutessani voinut säätää:

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

Mallin sopivuuden arviointi

Mallin sopivuutta arvioin keskivirheen ja selityskertoimen avulla.

RMSE (root mean squared error) eli keskivirhe lasketaan seuraavasti: lasketaan toteutuneiden havaintojen ja mallin ennustamien arvojen erotusten neliöt yhteen ja jaetaan havaintojen lukumäärällä (mean squared error); lopuksi otetaan neliöjuuri.

Mean squared error löytyy sklearn.metrics-kirjastosta:

from sklearn.metrics import mean_squared_error

y_train_predict = malli.predict(X_train)
rmse = (np.sqrt(mean_squared_error(y_train, y_train_predict)))
r2 = malli.score(X_train,y_train)

print('Mallin sopivuus opetusdataan')
print("--------------------------------------")
print('Keskivirhe: {}'.format(rmse))
print('Selityskerroin: {}'.format(r2))
print("n")

y_test_predict = malli.predict(X_test)
rmse = (np.sqrt(mean_squared_error(y_test, y_test_predict)))
r2 = malli.score(X_test, y_test)

print('Mallin sopivuus testidataan')
print('--------------------------------------')
print('Keskivirhe: {}'.format(rmse))
print('Selityskerroin: {}'.format(r2))

Mallin sopivuus opetusdataan
————————————–
Keskivirhe: 5.6371293350711955
Selityskerroin: 0.6300745149331701

Mallin sopivuus testidataan
————————————–
Keskivirhe: 5.137400784702911
Selityskerroin: 0.6628996975186953

Katson vielä kuviona, miten hyvin ennustaminen onnistuu testidatassa:

plt.scatter(y_test, y_test_predict)
plt.xlabel('y_test')
plt.ylabel('y_test_predict')

Malli on sitä parempi, mitä lähempänä suoraa viivaa kuvion pisteet ovat.

Mallin parantaminen

Edellä esimerkkinä laskettu malli on kelvollinen, mutta voisin parantaa mallia monin tavoin:

Asuntojen mediaanihinnat eivät ole normaalisti jakautuneet (jakauma on oikealle vino). Mallin parantamiseksi voisin kokeilla jompaa kumpaa seuraavista:

• pudotan jakauman yläpään suurimmat mediaanihinnat pois opetusdatasta
• muunnan mediaanihintoja paremmin normaalijakaumaa vastaaviksi.

Selittävien muuttujien ja mediaanihintojen välinen riippuvuus ei ollut aivan suoraviivainen. Tämä saattaisi korjaantua, jos muunnan mediaanihinnat paremmin normaalijakaumaa vastaaviksi. Tarvittaessa voin tehdä myös selittäville muuttujille muunnoksia tai voin valita malliksi ei-lineaarisen mallin.

Malliin voin myös lisätä selittäviä muuttujia. PTRATIO-muuttujan ottamista selittäväksi muuttujaksi kannattaisi kokeilla.

Jos teen korjauksia malliin, niin voin arvioida korjatun mallin sopivuutta vertaamalla sen keskivirhettä ja selityskerrointa tämän artikkelin malliin.

Lineaarinen regressio 2

Jos koneoppiminen ja sklearn (scikit-learn) -kirjasto ovat sinulle täysin uusia, niin lue ennen tätä artikkelia Lineaarinen regressio 1

Tämän artikkelin ohjelmakoodin ja tulosteet löydät GitHubista:

https://github.com/taanila/tilastoapu/blob/master/linreg2.ipynb

Jos kopioit koodia itsellesi, niin kannattaa käyttää GitHubia. Tästä artikkelista kopioidut koodit eivät välttämättä toimi oikein.

Tämän artikkelin esimerkeissä käytän datoja http://taanila.fi/mokki.xlsx ja http://taanila.fi/mokkinew.xlsx

Lineaarisella regressiomallilla voidaan ennustaa jatkuvaluonteisen muuttujan arvoja selittävien muuttujien avulla, jos selittävien muuttujien ja ennustettavan muuttujan välillä on likimain lineaarinen (suoraviivainen) riippuvuus.

Lineaarista regressiomallia voidaan pitää koneoppimisen mallina, jos kone oppii mallin parametrit olemassa olevan datan perusteella.

Tarkastelen esimerkkinä kuvitteellista aineistoa kesämökkien hinnoista. Hintaa selittävinä muuttujina ovat rantaviivan pituus metreinä, mökin pinta-ala neliömetreinä ja dikitominen muuttuja sähköliittymästä (1 = sähköliittymä, 0 = ei sähköliittymää).

Ohjelmakirjastojen tuonti

Tuon kuvailevasta analyysista tutut kirjastot (numpy-kirjastoa en tällä kertaa tarvitse):

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

Datan valmistelu

Luen datan Excel-tiedostosta dataframeen:

df=pd.read_excel('http://taanila.fi/mokki.xlsx')
df

Muodostan feature-matriisin selittävistä muuttujista ranta, pinta-ala ja sähkö. Selitettäväksi muuttujaksi (target) tulee hinta.

X=df[['ranta', 'pinta-ala','sähkö']]
y=df['hinta']

Mallin sovitus

Tuon lineaaristen mallien kirjastosta LinearRegression-mallin. Mukavuussyistä annan mallille nimeksi malli.

Sovitan mallin dataan fit-funktiolla.

from sklearn.linear_model import LinearRegression
malli=LinearRegression()
malli.fit(X,y)

Tuloksesta näen  mallin lähtötiedot, joita olisin halutessani voinut säätää:

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

Mallin vakiotermi:

malli.intercept_

-96.94145434036429

Selittävien muuttujien kertoimet:

malli.coef_

array([ 1.9750098 ,  2.77578415, 20.29877373])

Mallin sopivuuden arviointi

Mallin selityskerroin:

malli.score(X,y)

0.9819136190845801

Selityskertoimen mukaan 98,2 % hinnan varianssista voidaan selittää selittävien muuttujien avulla.

Mallin sopivuutta voin arvioida myös virhetermejä (ennusteen ero toteutuneeseen hintaan) tarkastelemalla:

plt.scatter(malli.predict(X), malli.predict(X)-y)
plt.hlines(y=0,xmin=50,xmax=250)
plt.xlabel('Ennuste')
plt.ylabel('Poikkeama todellisesta')

Virhetermit ovat melko satunnaisesti jakautuneet, mikä on hyvä asia.

Seuraavassa tarkastelen vielä pistekuviona toteutunutta hintaa ja mallin ennustamaa hintaa:

plt.scatter(df['hinta'], malli.predict(X))
plt.xlabel('Todellinen hinta')
plt.ylabel('Ennuste')

Ennustaminen

Mallin perusteella voin laskea hintaennusteita uudelle datalle, jota ei käytetty mallin laatimiseen:

Xuudet=pd.read_excel('http://taanila.fi/mokkinew.xlsx')
Xuudet['Hintaennuste']=malli.predict(Xuudet)
Xuudet

Perinteisempi regressiotuloste

Halutessani saan perinteisemmän regressiotulosteen statsmodels-kirjaston toiminnoilla:

import statsmodels.api as sm
X = sm.add_constant(X)
malli_sm = sm.OLS(y, X)
results = malli_sm.fit()
print(results.summary())

Lineaarinen regressio 1

Tämän artikkelin ohjelmakoodin ja tulosteet löydät GitHubista:

https://github.com/taanila/tilastoapu/blob/master/linreg1.ipynb

Jos kopioit koodia itsellesi, niin kannattaa käyttää GitHubia. Tästä artikkelista kopioidut koodit eivät välttämättä toimi oikein.

Tämän artikkelin esimerkeissä käytän dataa http://taanila.fi/linreg1.xlsx

Yleistä koneoppimisen malleista

Tästä artikkelista opit sklearn (scikit-learn) -ohjelmakirjaston koneoppimisen mallien käyttöliittymän pelkistetyn esimerkin avulla. Käyttöliittymä sklearn-kirjaston malleihin on yksinkertainen sisältäen seuraavat vaiheet:

Valmistele data

Ohjatun (supervised) oppimisen malleissa datasta täytyy erottaa selittävät muuttujat (feature-matriisi , x-muuttujat) ja selitettävä muuttuja (label, target, y-muuttuja).

Ohjaamattomissa (unsupervised) malleissa tarvitaan ainoastaan feature-matriisi.

Tuo malli ja säädä lähtötiedot

Esimerkiksi tässä artikkelissa käytettävä lineaarinen regressiomalli tuodaan seuraavasti:

from sklearn.linear_model import LinearRegression

Lineaaristen mallien kirjastosta siis tuodaan LinearRegression-malli. Mallin lähtötietojen säätäminen edellyttää käytettävän mallin tuntemusta. Jos et ole perehtynyt malliin, niin voit tyytyä lähtötietojen oletusarvoihin.

Sovita malli (fit)

Tässä vaiheessa suoritetaan varsinainen laskenta. Onneksi valmiit algoritmit hoitavat laskennan.

Arvioi mallin sopivuutta

Sopivuuden arviointiin on monia menetelmiä, esimerkiksi selityskertoimen laskeminen, visuaalinen tarkastelu tai mallin toimivuuden testaaminen testidatalla.

Ennusta (predict)

Ennakoivassa analytiikassa keskeisin vaihe on tietysti ennusteiden laskeminen uudelle datalle.

Lineaarinen regressio

Lineaarisella regressiomallilla voidaan ennustaa jatkuvaluonteisen muuttujan arvoja selittävien muuttujien avulla, jos selittävien muuttujien ja ennustettavan muuttujan välillä on likimain lineaarinen (suoraviivainen) riippuvuus.

Lineaarista regressiomallia voidaan pitää koneoppimisen mallina, jos kone määrittää (oppii) mallin parametrit olemassa olevan datan (training data) perusteella.

Ohjelmakirjastojen tuonti

Kuvailevasta analyysistä tutut peruskirjastot ovat tarpeen:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

Datan valmistelu

Tässä esimerkissä luen datan Excel-tiedostosta dataframeen:

df = pd.read_excel('linreg1.xlsx')
df

Yritän selittää myyntiä mainoskuluilla, joten määritän mainoskulut selittäväksi muuttujaksi (x) ja myynnin selitettäväksi muuttujaksi (y). Feature-matriisin täytyy olla mallia sovitettaessa dataframe-muodossa, joten teen muunnoksen to_frame-funktiolla.

x=df['Mainoskulut 1000 €']
X=df['Mainoskulut 1000 €'].to_frame() #feature-matriisi
y=df['Myynti 1000 €'] #target
plt.scatter(x,y)

Pistekaavion perusteella riippuvuus mainoskulujen ja myynnin välillä näyttää likimain lineaariselta (suoraviivaiselta).

Mallin sovitus

Tuon LinearRegression-mallin lineaaristen mallien kirjastosta ja nimeän sen yksinkertaisuuden vuoksi nimellä malli.

from sklearn.linear_model import LinearRegression
malli=LinearRegression()
malli.fit(X,y)

Tulosteena saan mallin lähtötiedot (joita olisin voinut halutessani säätää):

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

Mallin sovittamisen jälkeen voin katsoa mallin parametreja. Yksinkertaisen lineaarisen regression tapauksessa mallin parametrit ovat suoran kulmakerroin ja vakiotermi.

malli.coef_ #kulmakerroin

array([52.56756757])

Kulmakerroin tulee listamuodossa (array), koska mallissa voisi olla useampia selittäviä muuttujia ja näin ollen myös useampia kulmakertoimia.

malli.intercept_ #vakiotermi

46.486486486486505

Mallina on siis suora, jonka yhtälö: y = 52,568x + 46,486

Mallin sopivuuden arviointi

Mallin selityskertoimen saan:

malli.score(X,y)

0.7663982928521625

Voin siis todeta: 76,6 % myynnin varianssista voidaan selittää mainoskuluilla.

Voin tarkastella mallin sopivuutta myös graafisesti:

xfit=np.linspace(0.4,1.4) #50 arvoa tasavälein väliltä 0.4 - 1.4
Xfit=pd.DataFrame(xfit)
yfit=malli.predict(Xfit)
plt.scatter(x,y)
plt.plot(xfit,yfit)
plt.xlabel('Mainoskulut 1000 €')
plt.ylabel('Myynti 1000 €')

Ennustaminen

Jos mainoskuluihin suunnitellaan käytettäväksi 700, 800 tai 900 euroa, niin mallin mukaiset myyntiennusteet:

malli.predict([0.7, 0.8, 0.9])

array([83.28378378, 88.54054054, 93.7972973 ])

Yhteenveto

Yksinkertaisimmillaan tuodaan ja määritellään malli, sovitetaan malli ja ennustetaan:

from sklearn.linear_model import LinearRegression 

malli=LinearRegression() 

malli.fit(X,y)

malli.predict([0.7, 0.8, 0.9])

 

Data-analytiikka Pythonilla

Päivitetty 4.5.2023

Data-analytiikka antaa vastauksia kysymyksiin

Data-analytiikka on tavoitteellista toimintaa: tavoitteena on etsiä vastauksia kysymyksiin. Data-analytiikan avulla vastataan monenlaisiin kysymyksiin:

• Minkälainen ikäjakauma asiakkaillamme on?
• Mihin toimintamme osa-alueisiin asiakkaamme ovat tyytymättömiä?
• Onko asiakkaan iällä yhteyttä asiakastyytyväisyyteen?
• Miten yrityksen työilmapiiri on muuttunut viime vuodesta?
• Ketkä asiakkaistamme ovat vaarassa siirtyä kilpailijalle?
• Keille tuotteen markkinointikampanja kannattaa suunnata?
• Mikä mainosvaihtoehdoista tehoaa parhaiten kohderyhmään?
• Mitä oheistuotteita verkkokaupasta ostaneella kannattaa tarjota?
• Mikä on tuotteen ennustettu kysyntä ensi kuussa?
• Liittyykö vakuutuskorvaushakemukseen vakuutuspetos?
• Millä todennäköisyydellä laina-asiakas ei pysty maksamaan lainaansa takaisin?

Data

Tavoitteiden (kysymykset, joihin halutaan vastata) asettamisen jälkeen pitää selvittää minkälaista dataa tarvitaan. Data voi olla esimerkiksi:

• Yrityksen tietokannoista löytyvää dataa (esimerkiksi CRM- ja ERP-järjestelmistä).
• Erilaisten tiedontuottajien tarjoamaa ilmaista tai maksullista dataa.
• Varta vasten kyselytutkimuksella tai kokeellisella tutkimuksella kerättyä dataa.
• Erilaisten sensorien/mittalaitteiden automaattisesti tuottamaa dataa.

Blogissani rajoitun rakenteelliseen eli strukturoituun dataan. Rakenteellinen data on sellaista, joka voidaan tallentaa taulukkomuotoon. Yleisiä data-analytiikkaan sopivia tiedostomuotoja ovat pilkkueroteltu tekstimuoto (.csv) ja Excel-muoto (.xlsx). Tietokannoista data haetaan kyselyiden (SQL-kyselykieli) avulla. Nettikyselyohjelmista datan saa yleensä ulos pilkkuerotellussa tekstimuodossa tai Excel-muodossa.

Kun sopiva data on olemassa, niin datasta saadaan vastauksia kysymyksiin seuraavien vaiheiden kautta:

• Datan valmistelu
  
• Kuvaileva analytiikka
• Selittävä analytiikka; selittävään analytiikkaan liittyy usein tilastollisen merkitsevyyden testaaminen: tilastollinen merkitsevyys kertoo, millä varmuudella otoksessa havaittuja eroja ja riippuvuuksia voidaan yleistää isompaan perusjoukkoon, josta otos on otettu.
• Ennakoiva analytiikka; tähän käytetään usein koneoppimisen malleja.

Datan valmistelu

Datan valmistelulla tarkoitan datojen yhdistelyä, dataan tutustumista, datan siivoamista ja datan muunnoksia.

Datan valmistelu voi olla data-analytiikan aikaa vievin vaihe. Ensimmäiseksi kannattaa varmistaa datan taulukkomuotoisuus:

• muuttujien nimet / kenttien nimet / sarakeotsikot ovat ensimmäisellä rivillä
• datassa ei ole tarpeettomia tyhjiä rivejä tai sarakkeita
• kuhunkin tilastoyksikköön/havaintoyksikköön liittyvät tiedot ovat yhdellä rivillä.

Datan valmistelu voi sisältää muiden muassa seuraavia:

• Eri lähteistä peräisin olevien datojen yhdistely
• Muuttujien uudelleen nimeäminen: jatkotoimet sujuvat sutjakkaammin, jos nimet ovat lyhyitä ja helposti tunnistettavia
• Desimaalipilkkujen tarkistaminen: vaikka Suomessa desimaalipilkkuna käytetään pilkkua, niin Pythonissa täytyy käyttää pistettä
• Päivämäärien muuntaminen päivämääriksi tunnistettavaan muotoon
• Mittayksiköiden tarkistaminen ja tarvittavien muunnosten tekeminen
• Puuttuvien arvojen käsittely: poistetaanko puuttuvia arvoja sisältävät rivit, korvataanko puuttuvat arvot jollain, miten puuttuvia arvoja merkitään
• Uusien muuttujien laskeminen: esimerkiksi summamuuttuja useasta mielipidemuuttujasta, tilauksen hinta tilausmäärän ja yksikköhinnan avulla jne.
• Arvojen luokittelu ja uudelleenkoodaaminen: esimerkiksi ikäluokat iän arvoista.

Kuvaileva analytiikka

Datan kuvailu voi sisältää seuraavia:

• Lukumäärä- ja prosenttiyhteenvetojen laskeminen kategorisille muuttujille (frekvenssitaulukot)
• Luokiteltujen jakaumien laskeminen määrällisille muuttujille
• Tilastollisten tunnuslukujen laskeminen määrällisille muuttujille (keskiarvo, keskihajonta, viiden luvun yhteenveto)
• Prosenttimuutosten laskeminen aikasarjoille
• Aikasarjojen tarkastelu viivakaavioina
• Liukuvien keskiarvojen esittäminen aikasarjojen yhteydessä.

Kuvailun tuloksia kannattaa visualisoida ja havainnollistaa hyvin viimeistellyillä taulukoilla ja kaavioilla.

Selittävä analytiikka ja tilastollinen merkitsevyys

Selittävä analytiikka voi sisältää seuraavia:

• Tilastollisten tunnuslukujen vertailua eri ryhmissä
• Kategoristen muuttujien riippuvuuden tarkastelua ristiintaulukoimalla
• Määrällisten muuttujien välisten korrelaatioiden tarkastelua
• Havaittujen erojen ja riippuvuuksien tilastollisen merkitsevyyden tarkastelua.

Jos käytetty data on otos isommasta perusjoukosta, niin tulokset kuvaavat otosta. Jos tarkoituksena on arvioida koko perusjoukkoa, niin otoksessa havaittujen erojen ja riippuvuuksien tilastollinen merkitsevyys kertoo, millä varmuudella eroja ja riippuvuuksia voidaan yleistää otoksesta perusjoukkoon.

Ennakoiva analytiikka ja koneoppiminen

Koneoppimisen malleilla voidaan luokitella (asiakkaat luottoriski-asiakkaisiin ja muihin, vakuutuskorvaushakemukset selviin tapauksiin ja petokselta haiskahtaviin, sähköpostiviestit roskapostiin ja kunnollisiin viesteihin jne.) ja ennakoida määrällisen muuttujan arvoja (käytetyn auton hinta, tuleva kysyntä jne.). Koneoppiminen perustuu siihen, että kone oppii käytettävän mallin parametrit olemassa olevasta datasta ja tämän jälkeen mallia voidaan soveltaa uuteen dataan.

Koneoppimisalgoritmit voidaan luokitella  seuraavasti:

• Ohjattu oppiminen (supervised learning): Algoritmi opetetaan opetusdatalla (training data). Esimerkiksi roskapostisuodatin opetetaan sähköpostidatalla, jossa on erilaisia tietoja kustakin sähköpostiviestistä sekä tieto siitä oliko sähköpostiviesti roskapostia. Tämän datan perusteella muodostuu malli, jota käyttäen tulevista sähköpostiviesteistä voidaan tunnistaa roskapostiviestit.
• Ohjaamaton oppiminen (Unsupervised learning): Esimerkiksi asiakkaiden jakaminen asiakassegmentteihin asiakastietojen perusteella.
• Vahvistusoppiminen (Reinforcement learning): Algoritmi suorittaa toimia ja saa niistä palautetta palkkioiden ja rangaistusten muodossa. Algoritmi oppii saamistaan palkkioista ja rangaistuksista. Vahvistettua oppimista käytetään esimerkiksi robotiikassa.

Seuraavassa jaotellaan ohjattu ja ohjaamaton oppiminen edelleen alatyyppeihin:

Ohjattu oppiminen

Kohdemuuttuja kategorinen

Jos kohdemuuttuja (ennakoitava muuttuja) on kategorinen, niin kyseeseen tulevat luokittelua suorittavat algoritmit, esimerkiksi logistinen regressio tai päätöspuut.

Esimerkkejä, joissa on kategorinen kohdemuuttuja:

• Roskapostisuodatin: kohdemuuttujana on tieto siitä, onko sähköpostiviesti roskapostia vai ei?
• Lääketieteellinen diagnoosi: Kohdemuuttujana on tieto siitä, onko tutkitulla potilaalla tietty sairaus vai ei?
• Vakuutuspetosten tunnistaminen: Kohdemuuttujana on tieto siitä, liittyykö korvaushakemukseen petos vai ei?

Kohdemuuttuja määrällinen

Jos kohdemuuttuja on määrällinen, niin kyseeseen tulevat regressiomallit ja aikasarjaennustamisen menetelmät. Esimerkkejä, joissa on määrällinen kohdemuuttuja:

• Vanhan osakehuoneiston hinnan arviointi: Kohdemuuttujana on asunnon hinta.
• Kysynnän ennustaminen aikaisemman kysynnän perusteella: Kohdemuuttujana on kysyntä.

Ohjaamaton oppiminen

Ohjaamattoman oppimisen algoritmi muodostaa mallin suoraan datasta (ei siis ole erillistä opetusdataa, jossa olisi valmiina kohdemuuttujan arvoja). Esimerkkinä asiakassegmenttien määrittäminen asiakasdatan pohjalta. Paljon käytetty algoritmi on k-means clustering.

Jos datassa on paljon muuttujia, jotka mittaavat osittain samoja asioita, niin datan rakennetta voidaan yksinkertaistaa yhdistämällä muuttujia uusiksi lasketuiksi muuttujiksi, joita on vähemmän kuin alkuperäisiä muuttujia. Tunnetuin algoritmi tähän tarkoitukseen on pääkomponenttianalyysi.

Aikasarjaennustaminen 3

Päivitetty 29.12.2020

Tämä artikkeli on jatkoa artikkeleille Aikasarjaennustaminen 1 ja Aikasarjaennustaminen 2.

Edellisen artikkelin Aikasarjaennustaminen 2 lopussa totesin, että esimerkkinä käyttämässäni aikasarjassa on neljän vuosineljänneksen välein toistuvaa kausivaihtelua, joka on syytä huomioida ennustamisessa. Tässä artikkelissa tarkastelen kausivaihtelun huomioivaa Holt-Winterin menetelmää.

Holt-Winterin tulomallissa aikasarjan tason L (level) hetkellä t määrittää lauseke

L_t = alfa * Y_t/S_t-s + (1 – alfa)(L_t-1 + T_t-1)

Yllä Y_t on viimeisin havainto, S_t-s on edellisen vastaavan periodin kausivaihtelu ja  T_t-1 on edellinen trendi.

Trendille T hetkellä t saadaan arvio lausekkeesta

T_t = beta * (L_t – L_t-1) + (1 – beta) * T_t-1

Kausivaihtelulle S hetkellä t saadaan arvio lausekkeesta

S_t = gamma * Y_t/L_t + (1 – gamma) * S_t-s

Ennuste hetkelle t + p saadaan

(L_t + pT_t)S_t-s

Yllä on kyse Holt-Winterin tulomallista, jossa kausivaihtelu huomioidaan kausivaihtelukertoimena. Holt-Winterin mallia voidaan soveltaa myös summamallina, jolloin kausivaihtelu huomioidaan lisättävänä kausivaihteluterminä. Tulomalli soveltuu paremmin tilanteisiin, joissa kausivaihtelukomponentin suuruus vaihtelee aikasarjan tason L mukaan. Summamalli soveltuu tilanteisiin, joissa kausivaihtelukomponentin suuruus ei riipu aikasarjan tasosta L.

Mallin parametrit alfa, beta ja gamma pyritään määrittämään siten että ennustevirheiden neliöiden keskiarvo saadaan mahdollisimman pieneksi.

Python toteutus

Esimerkkikoodin kolminkertaiseen eksponentiaaliseen tasoitukseen löydät GitHubista:

https://nbviewer.jupyter.org/github/taanila/aikasarjat/blob/main/forecast3.ipynb

Aikasarjaennustaminen 2

Päivitetty 29.12.2020

Tämä artikkeli on jatkoa yksinkertaista eksponentiaalista tasoitusta käsittelevälle artikkelille Aikasarjaennustaminen 1. Tässä artikkelissa käytän kaksinkertaista eksponentiaalista tasoitusta eli Holtin mallia, joka huomioi myös trendin.

Holtin mallissa aikasarjan tason L (level) hetkellä t määrittää lauseke

L_t = alfa * Y_t + (1 – alfa) * (L_t-1 + T_t-1)

Yllä Y_t on viimeisin havainto ja T_t-1 on edellinen trendi. Trendille hetkellä t saadaan arvio lausekkeesta

T_t = beta * (L_t – L_t-1) + (1 – beta) * T_t-1

Ennuste hetkelle t+p saadaan

L_t + pT_t

Mallin parametrit alfa ja beta pyritään määrittämään siten että ennustevirheiden neliöiden keskiarvo saadaan mahdollisimman pieneksi.

Python toteutus

Esimerkkikoodin kaksinkertaisen eksponentiaalisen tasoituksen käytöstä löydät GitHubista:

https://nbviewer.jupyter.org/github/taanila/aikasarjat/blob/main/forecast2.ipynb

Aikasarjan lähempää tarkastelua

Löytääkseni paremman ennustemallin tarkastelen esimerkkikoodissa käyttämääni aikasarjaa hieman lähemmin purkamalla sen komponentteihin.

from statsmodels.tsa.api import seasonal_decompose
seasonal_decompose(data['Demand']).plot()

Tuloksena saan neljä kuviota:

• alkuperäinen aikasarja
• aikasarjasta erotettu trendi
• aikasarjan kausivaihtelu
• aikasarjan jäljelle jäänyt osa trendin ja kausivaihtelun poistamisen jälkeen.

Aikasarjassa on erotettavissa selkeä neljän vuosineljänneksen jaksoissa toistuva kausivaihtelu, jota kaksinkertainen eksponentiaalinen tasoitus ei huomioi ennusteessa. Asiaa voin tarkastella myös autokorrelaatioiden avulla. Autokorrelaatio tarkoittaa aikasarjan korrelaatiota viivästetyn aikasarjan kanssa, esimerkiksi aikasarjan korrelaatio neljän vuosineljänneksen takaisiin aikasarjan arvoihin. Autokorrelaatio voidaan laskea eri viiveille. Tämän voin tehdä pandas-kirjaston autocorrelation_plot-toiminnolla:

from pandas.plotting import autocorrelation_plot
autocorrelation_plot(data['Demand'])

Vaaka-akselilla on viive (lag) ja pystyakselilla autokorrelaatiokertoimen arvo. Huomaan, että viiveen 4 kohdalla on suurehko korrelaatio. Tämä viittaa neljän vuosineljänneksen mittaiseen kausivaihtelujaksoon. Kuvion katkoviivat edustavat tilastollisesti merkitsevän korrelaation rajoja. Viiveen 4 kohdalla korrelaatio on katkoviivan yläpuolella ja näin ollen tilastollisesti merkitsevä.

Seuraavassa artikkelissa Aikasarjaennustaminen 3 laadin ennustemallin, jossa myös neljän vuosineljänneksen jaksoissa toistuva kausivaihtelu on huomioitu.

Aikasarjaennustaminen 1

Päivitetty 29.12.2020

Aikasarjaennustamisessa oletan että toteutuneiden havaintojen muodostama aikasarja sisältää informaatiota, joka auttaa tulevien havaintojen ennustamisessa. Ennustusmenetelmä riippuu siitä, minkälaista systemaattista vaihtelua aikasarjassa esiintyy. Eksponentiaalisia tasoitusmenetelmiä käytettäessä on kolme päävaihtoehtoa:

• Yksinkertainen eksponentiaalinen tasoitus aikasarjoille, joissa ei ole trendiä eikä kausivaihtelua.
• Kaksinkertainen eksponentiaalinen tasoitus eli Holtin menetelmä aikasarjoille, joissa on trendi, mutta ei kausivaihtelua.
• Kolminkertainen eksponentiaalinen tasoitus eli Holt-Winterin menetelmä aikasarjoille, joissa on sekä trendi että kausivaihtelu.

Tämä artikkeli käsittelee yksinkertaista eksponentiaalista tasoitusta. Yksinkertaisessa eksponentiaalisessa tasoituksessa ennuste lasketaan seuraavasti:

alfa*edellinen havainto + (1 – alfa)*edellinen ennuste

Ennuste saadaan viimeisimmän havainnon ja siihen liittyneen ennusteen painotettuna summana. Painokerroin alfa on välillä 0 – 1 oleva luku, joka ilmaisee, kuinka suurella painolla edellistä havaintoa painotetaan ennustetta laskettaessa:

• • Jos alfa on 0, niin ennuste on sama kuin edellinen ennuste.
  • Jos alfa on 1, niin ennuste on sama kuin edellinen havainto.
  • Suuret alfan arvot antavat ennusteita, jotka reagoivat herkästi aikasarjassa esiintyvään vaihteluun, koska viimeisimmillä havainnoilla on suuri paino.
  • Pienet alfan arvot tasoittavat voimakkaasti aikasarjan vaihtelua.

Alfan arvo valitaan yleensä siten että ennustevirheiden neliöiden keskiarvo saadaan mahdollisimman pieneksi. Voin kirjoittaa ennusteen laskentakaavan myös muotoon

edellinen ennuste + alfa*(edellinen havainto – edellinen ennuste)

Ennustetta siis korjataan jokaisen toteutuneen havainnon jälkeen korjaustermillä alfa*edellisen ennusteen virhe.

Python toteutus

Esimerkkikoodin yksinkertaisen eksponentiaalisen tasoituksen käyttöön löydät GitHubista:

https://nbviewer.jupyter.org/github/taanila/aikasarjat/blob/main/forecast1.ipynb

Seuraavaksi

Esimerkkinä käyttämässäni aikasarjassa on melko helppo erottaa alkupään laskeva trendi ja loppupään nouseva trendi. Seuraavassa artikkelissani Aikasarjaennustaminen 2 yritän sovittaa aikasarjaan mallin, joka huomioi trendin.

Merkitsevyyden testaus Pythonilla

Tämän artikkelin ohjelmakoodin ja tulosteet löydät GitHubista:

https://github.com/taanila/tilastoapu/blob/master/p.ipynb

Jos kopioit koodia itsellesi, niin kannattaa käyttää GitHubia. Tästä artikkelista kopioidut koodit eivät välttämättä toimi oikein.

Oletan, että lukijalla on asennettuna Anaconda ja sen mukana tuleva Jupyter notebook.

Otoksessa havaitsemieni erojen ja riippuvuuksien tilastollista merkitsevyyttä voin arvioida laskemalla p-arvon. Pythonin scipy.stats-ohjelmakirjastosta löydän funktiot p-arvojen laskentaan.

Otan ensiksi käyttöön pandas ja scipy.stats -ohjelmakirjastot ja avaan esimerkkinä käyttämäni aineiston:

import pandas as pd
import scipy.stats as stats

df = pd.read_excel('http://taanila.fi/data1.xlsx', 
   sheet_name = 'Data')
df.head()

Korrelaatiokertoimen testaus

Iän ja palkan välisen pearsonin korrelaatiokertoimen ja siihen liittyvän 2-suuntaisen p-arvon saan funktiolla

stats.pearsonr(df['ikä'], df['palkka'])

Jos haluankin käyttää spearmanin järjestyskorrelaatiota, niin saan korrelaatiokertoimen ja 2-suuntaisen p-arvon funktiolla

stats.spearmanr(df['ikä'], df['palkka'])

Korrelaatiokertoimen testaamiseen liittyvistä funktioista löydät lisätietoa scipy.org -sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pearsonr.html#scipy.stats.pearsonr

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.spearmanr.html

Ristiintaulukointi ja khiin neliö -testi

Esimerkiksi sukupuolen ja perhesuhteen väliseen ristiintaulukointiin liittyvän khiin neliö -testin testimuuttujan, p-arvon, vapausasteiden määrän ja odotetut frekvenssit saan funktiolla:

stats.chi2_contingency(pd.crosstab(df['sukup'], 
   df['perhe']))

Lisätietoa khiin neliö -testistä ja sen edeltävyysehdoista löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html#scipy.stats.chi2_contingency

Kahden riippumattoman otoksen t-testi

Jos haluan selvittää, onko miesten ja naisten palkkakeskiarvoissa eroa, niin erotan ensin miesten ja naisten palkat toisistaan (aineistossa 1=mies, 2=nainen)

a=df['palkka'][df['sukup']==1] #Mies
 b=df['palkka'][df['sukup']==2] #Nainen

Tämän jälkeen lasken t-testimuuttujan ja 2-suuntaisen p-arvon funktiolla

stats.ttest_ind(a, b, equal_var=False)

Yllä käytin erisuurten varianssien testiä (equal_var=False).

Lisätietoa riippumattomien otosten t-testistä ja sen edeltävyysehdoista löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html

Mann Whitney U -testi

Jos epäilen t-testin edeltävyysehtojen toteutumista, niin voin testata edellisen esimerkin Mann Whitney U-testillä:

stats.mannwhitneyu(a,b)

Tuloksena saan U-testimuuttujan ja p-arvon. Oletuksena saan 2-suuntaisen p-arvon puolikkaan. Lisätietoa löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.mannwhitneyu.html

Yksisuuntainen varianssianalyysi

Jos haluan selvittää onko eri koulutuksen omaavien keskipalkoissa eroja, niin voin käyttää yksisuuntaista varianssianalyysiä (anova).  Ensiksi erotan eri koulutuksen omaavien palkat toisistaan:

k1=df['palkka'][df['koulutus']==1] #peruskoulu
k2=df['palkka'][df['koulutus']==2] #2. aste
k3=df['palkka'][df['koulutus']==3] #korkeakoulu
k4=df['palkka'][df['koulutus']==4] #ylempi korkeakoulu

Tämän jälkeen lasken anovan F-testimuuttujan ja p-arvon funktiolla:

stats.f_oneway(k1,k2,k3,k4)

Lisätietoa anovasta ja sen edeltävyysehdoista löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.f_oneway.html#scipy.stats.f_oneway

Kruskal-Wallis -testi

Jos epäilet varianssianalyysin edeltävyysehtojen  täyttymistä edellisessä esimerkissä, niin voit käyttää varianssianalyysin sijasta Kruskal-Wallis -testiä:

stats.kruskal(k1, k2, k3, k4)

Tuloksena saat H-testimuuttujan ja p-arvon.

Lisätietoa Kruskal-Wallis-testistä löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kruskal.html#scipy.stats.kruskal

Muita testejä

Lisää merkitsevyystestejä ja muita tilastollisia funktioita löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/stats.html

 

 

 

 

Jupyter Notebook

Päivitetty 14.4.2024

Jupyter Notebook on kätevä väline data-analytiikkaan liittyvien Python-ohjelmien kirjoittamiseen ja suorittamiseen. Myös monissa pilvipalveluissa toimivat muistikirja-tyyppiset ohjelmointiympäristöt (esimerkiksi Google Colab) perustuvat Jypyter Notebookiin.

Käynnistä Jupyter Notebook

Minicondassa Jupyter käynnistyy komentoriviltä komennolla jupyter notebook.

Anacondassa se löytyy Windowsin käynnistysvalikosta Anacondan alta.

Jupyter Notebookin etusivu käynnistyy oletusselaimeesi Home-nimiselle välilehdelle.

Luo uusi muistio

Voit luoda uuden tyhjän muistion Jupyterin etusivun oikean yläreunan New – Python 3 -tai New – Notebook -toiminnolla. Uusi muistio avautuu selaimeen uudelle välilehdelle.

Muistion yläreunasta löydät työkalupainikkeita ja valikoita, joiden sisältöön kannattaa heti alussa tutustua. Muistion voit nimetä uudelleen File-valikon Rename-toiminnolla tai napsauttamalla muistion nimeä muistion yläreunassa.

Kirjoita koodia

Muistio koostuu soluista. Soluun voit kirjoittaa Python-koodia ja kommentteja. Kommenttirivi alkaa aina #-merkillä. Koodin voit suorittaa usealla tavalla:

• Run-valikon kautta
• työkalurivin painikkeella
• näppäinyhdistelmällä ctrl-enter tai shift-enter (siirtää kohdistimen samalla seuraavaan soluun). Lisää pikanäppäimiä löydät googlaamalla Jupyter keyboard shortcuts.

Koodin suorituksesta mahdollisesti seuraavat tulokset, varoitukset ja virheilmoitukset tulostuvat solun alapuolelle. Voit milloin tahansa muuttaa solun koodia ja suorittaa koodin uudelleen.

Uusia soluja voit lisätä Insert-valikon kautta ja soluja voit tuhota Edit-valikon kautta.

Aiemmin suorittamasi koodin tallentamat muuttujat ym. tiedot säilyvät koko istunnon ajan. Voit näin ollen suorittaa osan ohjelmasta yhdessä solussa ja jatkaa ohjelman suoritusta toisessa solussa.

Jos muokkaat ja suoritat uudelleen aiempia koodisoluja, niin ajaudut helposti ennakoimattomiin virhetilanteisiin. Voit milloin tahansa suorittaa kaikkien solujen komennot uudelleen Run-valikon Run All -toiminnolla.

Jos avaat ja jatkat aiemmin aloittamaasi muistiota, niin suorita aiemmin kirjoittamasi koodi valitsemalla Run-valikosta Run All.

Tallenna muistio

Muistio tallentuu automaattisesti, mutta varmuuden vuoksi kannattaa napsauttaa tallennus-kuvaketta ennen muistion sulkemista. Näin viimeisin versio on varmuudella tallessa.

Muistio tallentuu Jupyterin oletuskansioon. Minun Windows-koneellani oletuskansiona on C:/Users/aki/ (aki on minun käyttäjätunnukseni). Jupyter Notebook -tiedoston (muistion) tunnistat tiedostonimen loppuosasta .ipynb. Tallentamasi muistiot löydät Jypyterin etusivulta (Home-välilehti) ja voit avata muistion omalle välilehdelleen napsauttamalla muistion nimeä.

Voit luoda oletuskansion alle uusia kansioita. Voit siirtyä toiseen kansioon napsauttamalla Jupyterin etusivulla (Home-välilehti) kansion nimeä. Uusi muistio tallentuu aina siihen kansioon, joka on valittuna muistion luontihetkellä.

Opettele Pythonin perusteet

Voit aloittaa suoraan data-analytiikasta muistion pandas1 avulla. Parhaiten opit kirjoittamalla muistion koodit itse Jupyter-muistioon ja tekemällä siinä ohessa omia kokeiluja. Sinulla ei tarvitse olla aiempaa ohjelmointikokemusta! Voit käyttää tukena muistioon pandas1 liittyvää videota.

Suosittelen myös Pythonin perusteisiin tutustumista Teemu Sirkiän mainion materiaalin avulla: http://www.cs.hut.fi/~ttsirkia/Python.pdf

Asenna Miniconda tai Anaconda

Päivitetty 6.2.2024

Data-analytiikkaan tarvittavat Python-taidot voit oppia nopeasti vaikket omaisikaan aiempaa ohjelmointikokemusta.

Ensimmäiseksi tarvitset data-analytiikkaan sopivan muistikirja-tyyppisen ohjelmointiympäristön.

Jos et halua asentaa ympäristöä omalle koneellesi, niin voit käyttää esimerkiksi ilmaista Google Colab -pilvipalvelua osoitteessa https://colab.research.google.com/. Palvelun käyttämiseen tarvitset Google-tunnuksen.

Omalle koneelle asennettavaksi ympäristöksi sopii Miniconda tai Anaconda.

Miniconda

Voit katsoa Minicondan asennuksen kulun videolta.

Miniconda sisältää Pythonin ja conda-paketinhallintajärjestelmän. Minicondan asennus sujuu nopeasti ja se vie tilaa vähemmän kuin Anaconda.

Löydät Minicondan Windowsille, Macille ja Linuxille osoitteesta

https://docs.conda.io/en/latest/miniconda.html

Valitse oma käyttöjärjestelmäsi (Windows, macOS tai Linux) ja asenna Miniconda oletusasetuksilla.

Käynnistä asennuksen jälkeen Anacondan komentorivi:

• Windows-koneilla Miniconda3 – Anaconda prompt (miniconda3) Windowsin käynnistysvalikosta
• MacOS- ja Linux-koneilla terminal/pääte.

Komentorivillä voit asentaa tarvitsemasi kirjastot/paketit. Jokaisen asennuskomennon jälkeen kestää hetken ennen kuin conda löytää sinulle sopivan version, jonka jälkeen se kysyy vielä lupaa asennukseen. Vastaa kysymykseen y-kirjaimella (ja paina enter). Data-analytiikkaa varten tarvitset ainakin seuraavat:

• conda install jupyter (Jupyter Notebook on data-analytiikassa suosittu ohjelmointiympäristö).
• conda install pandas (data-analytiikan peruskirjasto, jonka mukana asentuu myös numeerisen laskennan peruskirjasto numpy).
• conda install seaborn (grafiikka-kirjasto, jonka mukana asentuu myös grafiikan peruskirjasto matplotlib).
• conda install scikit-learn (koneoppimisen kirjasto, jonka mukana asentuu myös tieteellisen laskennnan peruskirjasto scipy).
• conda install statsmodels (tilastollisten mallien kirjasto mm. aikasarjaennustamiseen).
• conda install xlwings (kirjasto Excelin ohjaamiseen).
• conda install openpyxl (Excel-tiedostojen avaamiseen).
• conda install xlsxwriter (Excel-tiedostojen kirjoittamiseen).

Myöhemmin voit tarpeen mukaan asentaa muita kirjastoja.

Anaconda

Anaconda sisältää muiden muassa

• Pythonin
• datojen analysointiin tarvittavat ohjelmakirjastot (NumPy, pandas, jne.)
• graafiseen esittämiseen tarvittavat ohjelmakirjastot (matplotlib, seaborn jne.)
• koneoppimisen malleihin tarvittavat ohjelmakirjastot (scikit-learn jne.)
• Jupyter Notebookin ohjelmien kirjoittamiseen ja suorittamiseen
• Conda-paketinhallintajärjestelmän, jolla voit asentaa ja päivittää ohjelmakirjastoja (paketteja) siten että kirjastojen versiot ovat keskenään yhteensopivia.

Löydät Anacondan Windowsille, Macille ja Linuxille osoitteesta

https://www.anaconda.com/products/distribution

Valitse oma käyttöjärjestelmäsi (Windows, macOS tai Linux) ja asenna Anaconda oletusasetuksilla.

Ohjeita Anacondan käyttöön löydät osoitteesta

https://docs.anaconda.com/anaconda/

Anaconda sisältää paljon kirjastoja, joita et koskaan tarvitse. Jos haluat asentaa vain tarvitsemasi, niin asenna Anacondan sijasta Miniconda.

Asennuksen jälkeen

Tutustu asennuksen jälkeen Jupyter notebookin toimintaan.

Määrälliset muuttujat pivot-kaaviona

Päivitetty 6.2.2019

• pivotchart3.xlsx

Olethan opetellut artikkelissa Pivot-kaaviot kuvatut toimet ennen tämän artikkelin lukemista?

Määrälliset muuttujat mittaavat määrää: euroja, vuosia, metrejä, kiloja jne.

Seuraavien esimerkkien aineistot ja pivot-taulukot löydät tiedostosta pivotchart3.xlsx.

Ryhmittely

Jos haluan laskea määrällisen muuttujan arvojen esiintymiskertoja, niin yleensä tarvitsen ryhmittelyä. Tarkastelen esimerkkinä ikäjakauman esittämistä. Esimerkkiaineistona käytän tiedoston pivotchart3.xlsx Data-aineistoa.

• Valitsen yhden ja vain yhden solun aineiston alueelta.
• Valitsen Insert-välilehdeltä PivotChart. Jos en vaihda Create PivotChart -ikkunan asetuksia, niin pivot-kaaviota varten muodostuu uusi taulukko (Sheet). Uudessa taulukossa ovat paikkavaraukset pivot-taulukolle ja pivot-kaaviolle.
• Pivot-kaavion rakenteen määrittelen PivotChart Fields -kenttäluettelossa, joka on näkyvillä pivot-kaavion ollessa valittuna.
• Raahaan ikä-muuttujan Values-ruutuun.
• Vaihdan laskentaperusteeksi Sum sijasta Count.
• Raahaan ikä-muuttujan Axis (Categories) -ruutuun.
• Valitsen pivot-taulukosta solun, jossa on ensimmäinen ikä (20).
• Valitsen Analyze-välilehdeltä Group Field (Ryhmän kenttä).

• Grouping-ikkunassa voin tarvittaessa vaihtaa Excelin ehdottamia ryhmittelyn aloituskohtaa, päättymiskohtaa ja ryhmävälin suuruutta.

Räätälöity ryhmittely

Edellä kuvaamallani Group Field -toiminnolla saan vain tasavälisiä ryhmittelyitä, joissa ryhmävälin suuruus on sama kaikissa ryhmissä. Seuraavassa määrittelen iälle ryhmittelyn 20-29, 30-39, 40-49, 50+. Jatkan suoraan edellisen esimerkin pivot-kaaviosta.

• Poistan aiemman iän ryhmittelyn (valitsen pivot-taulukosta ensimmäisen ikäryhmän solun ja valitsen Analyze-Ungroup (Pura ryhmittely).
• Valitsen pivot-taulukosta solut, joissa on iät 20-29.
• Valitsen Analyze-Group Selection (Ryhmän valinta).
• Valitsen pivot-taulukosta solut, joissa on iät 30-39.
• Valitsen Analyze-Goup Selection.
• Toistan edellä kuvattuja vaiheita kunnes kaikki ryhmät on luotu.

Excel nimeää ryhmät Group1, Group2, jne. Voin kirjoittaa nimien tilalle kuvaavammat nimet. Ryhmän nimen vieressä on -/+ -painike, josta voin piilottaa tai näyttää ryhmän yksityiskohtaiset tiedot.

Seuraavassa olen nimennyt ensimmäisen ryhmän 20-29 ja olen piilottanut kolmen ensimmäisen ryhmän yksityiskohtaiset tiedot. Huomaa, että pivot-kaavio näyttää tiedot sellaisena kuin ne ovat pivot-taulukossa.

Itselläni on tapana tehdä ryhmittelyt etukäteen alkuperäiseen aineistoon. Lue lisää artikkelista Muuttujan arvojen ryhmittely ja muuttaminen.

Keskiarvo

Seuraavassa lasken palkkakeskiarvot koulutuksen mukaan:

• Valitsen yhden ja vain yhden solun aineiston alueelta.
• Valitsen Insert-välilehdeltä PivotChart. Jos en vaihda Create PivotChart -ikkunan asetuksia, niin pivot-kaaviota varten muodostuu uusi taulukko (Sheet). Uudessa taulukossa ovat paikkavaraukset pivot-taulukolle ja pivot-kaaviolle.
• Pivot-kaavion rakenteen määrittelen PivotChart Fields -kenttäluettelossa, joka on näkyvillä pivot-kaavion ollessa valittuna.
• Raahaan palkka-muuttujan Values-ruutuun.
• Vaihdan laskentaperusteeksi Count sijasta Average.
• Raahaan koulutus-muuttujan Axis (Categories) -ruutuun.
• Siirrän pivot-taulukon Peruskoulu-solun 2. aste -solun yläpuolelle, jolloin koulutukset menevät koulutuksen pituuden mukaiseen järjestykseen.

Viimeistelyn jälkeen pivot-kaavio voisi näyttää seuraavalta:

Vastausten lukumäärät (n) kirjoitin riviotsikoihin. Sain lukumäärät selville vaihtamalla hetkeksi laskentaperusteeksi Average sijasta Count.

Summa

Summa on käyttökelpoinen yhteenvetotapa esimerkiksi myyntitietojen yhteydessä. Seuraavassa käytän tiedoston pivotchart3.xlsx aineistoa Myynnit.

• Valitsen yhden ja vain yhden solun aineiston alueelta.
• Valitsen Insert-välilehdeltä PivotChart. Jos en vaihda Create PivotChart -ikkunan asetuksia, niin pivot-kaaviota varten muodostuu uusi taulukko (Sheet). Uudessa taulukossa ovat paikkavaraukset pivot-taulukolle ja pivot-kaaviolle.
• Pivot-kaavion rakenteen määrittelen PivotChart Fields -kenttäluettelossa, joka on näkyvillä pivot-kaavion ollessa valittuna.
• Raahaan Hinta-muuttujan Values-ruutuun. Laskentaperuste on valmiiksi Sum, koska jokaisella rivillä on arvo Hinta-muuttujalla.
• Raahaan Myyjä-muuttujan Axis (Categories) -ruutuun.

Voin järjestää myyntisummat suuruusjärjestykseen valitsemalla Pivot-taulukon tai Pivot-kaavion pudotusvalikosta More Sort Options ja järjestämällä Sum of Hinta -mukaiseen järjestykseen. Viimeistelyn jälkeen pivot-kaavio voisi näyttää seuraavalta:

Monivalinta pivot-kaaviona

Päivitetty 6.2.2019

• pivotchart2.xlsx

Olethan opetellut artikkelissa Pivot-kaaviot kuvatut toimet ennen tämän artikkelin lukemista?

Monivalintakysymyksessä tarjotaan useita vaihtoehtoja, joista vastaaja voi valita useammankin kuin yhden. Jokainen monivalinnan vaihtoehto tallennetaan aineistoon omana sarakkeenaan. Jos vaihtoehto on valittu, niin aineistossa on arvo 1, muussa tapauksessa aineistoon voidaan jättää tyhjä kohta.

Seuraavassa käytän esimerkkinä kyselytutkimusaineistoa, jossa on kysytty työntekijän hyödyntämiä etuisuuksia: työterveyshuolto, lomaosake, kuntosali, hieroja. Esimerkkiaineisto ja pivot-kaaviot löytyvät tiedostosta pivotchart2.xlsx.

• Valitsen yhden ja vain yhden solun aineiston alueelta.
• Valitsen Insert-välilehdeltä PivotChart. Jos en vaihda Create PivotChart -ikkunan asetuksia, niin pivot-kaaviota varten muodostuu uusi taulukko (Sheet). Uudessa taulukossa ovat paikkavaraukset pivot-taulukolle ja pivot-kaaviolle.
• Pivot-kaavion rakenteen määrittelen PivotChart Fields -kenttäluettelossa, joka on näkyvillä pivot-kaavion ollessa valittuna.
• Raahaan työterveyshuolto-muuttujan Values-ruutuun.
• Raahaan lomaosake-muuttujan Values-ruutuun.
• Raahaan kuntosali-muuttujan Values-ruutuun.
• Raahaan hieroja-muuttujan Values-ruutuun.

Tässä vaiheessa lasketut arvot ovat pivot-taulukossa sarakkeittain, koska Excel on sijoittanut Values-palikan Legend (Series)-ruutuun. Pivot-kaaviossa tämä näkyy siten, että jokainen pylväs muodostaa oman arvosarjansa ja näkyy omalla värillään.

• Raahaan Legend (Series)-ruudun Values-palikan Axis (Categories)-ruutuun.
• Kirjoitan pivot-taulukkoon monivalinnan vaihtoehtojen nimet nimien Count of työterveyshuolto jne. tilalle. Excel ei kelpuuta muuttujan nimenä esiintyvää työterveyshuolto pivot-taulukon riviotsikoksi, joten lisään nimen perään välilyönnin.

Yleensä monivalinnan pylväät kannattaa järjestää pituusjärjestykseen.

• Napsautan hiiren oikeaa painiketta jonkin pivot-taulukon lukumäärän päällä ja valitsen Sort – Sort Largest to Smallest.

Pienen viimeistelyn jälkeen pivot-kaavio voisi näyttää seuraavalta.

Jos haluan tarkastella asiaa ryhmittäin esimerkiksi sukupuolen mukaan, niin voin vielä raahata ryhmittelevän muuttujan Legend (Series) -ruutuun.

Pivot-kaaviot

Päivitetty 6.2.2019

• pivotchart.xlsx

Tässä artikkelissa kirjoitan pylväskaavioista. Oletan, että osaat jo entuudestaan laatia ja muotoilla pylväskaavioita. Jollet osaa, niin opit perusasiat itseopiskelupaketista kaavio.xlsx.

Pivot-kaavioilla laadin nopeasti monipuolisia yhteenvetoja isosta aineistosta. Aineiston täytyy olla asianmukaiseen muotoon tallennettu artikkelin Tilastoaineiston tallentaminen mukaisesti. Tämän artikkelin esimerkeissä käytetyn aineiston ja pivot-kaaviot löydät tiedostosta pivotchart.xlsx.

Yksinkertainen pivot-kaavio

Tarkastelen pivot-kaaviota, josta näen kuinka moni työntekijä on kuinkakin tyytyväinen johtoon:

• Valitsen yhden ja vain yhden solun aineiston alueelta.
• Valitsen Insert-välilehdeltä PivotChart – PivotChart & PivotTable. Jos en vaihda Create PivotChart -ikkunan asetuksia, niin pivot-kaaviota varten muodostuu uusi taulukko (Sheet). Uudessa taulukossa ovat paikkavaraukset pivot-taulukolle ja pivot-kaaviolle.
• Pivot-kaavion rakenteen määrittelen PivotChart Fields (Pivot-kaavion kentät) -kenttäluettelossa, joka on näkyvillä pivot-kaavion ollessa valittuna.
• Raahaan tyytyväisyys johtoon -muuttujan Values-ruutuun. Excel laskee havaintojen lukumäärän (jos havaintoja puuttuu) tai havaintojen summan (jos jokaisella aineiston rivillä on havainto). Muuttujan tyytyväisyys johtoon -tapauksessa Excel laskee havaintojen summan. Muutan tämän lukumääräksi.
• Napsautan Values-ruutuun raahaamaani palikkaa. Valitsen esiin tulevasta pudotusvalikosta Value Field Settings (Arvokentän asetukset).
• Valitsen Value Field Settings -ikkunassa laskentaperusteeksi Count (Määrä) ja napsautan OK.

Tässä vaiheessa pivot-kaavion pylväs esittää havaintojen lukumäärän.

Raahaan tyytyväisyys johtoon -muuttujan Axis (Categories) (Akseli) -ruutuun. Axis (Categories) on tarkoitettu kaavion luokka-akselin luokille. Tässä tapauksessa luokkia ovat muuttujan tyytyväisyys johtoon arvot 1, 2, 3, 4 ja 5. Arvojen sanalliset selitteet kirjoitan suoraan Pivot-taulukkoon numeroiden 1, 2, 3, 4 ja 5 tilalle.

Viimeistelyn jälkeen kaavio voisi näyttää seuraavalta:

Tavallisista kaavioista poiketen pivot-kaaviossa on ylimääräisiä ”painikkeita”, joiden avulla voin lajitella ja suodattaa. Jos kaavio on valittuna, niin voin piilottaa ylimääräiset painikkeet valitsemalla Analyze-välilehdeltä Field Buttons – Hide All (Kenttäpainikkeet – Piilota kaikki).

Ryhmitelty pivot-kaavio

Jos raahaan sukupuoli-muuttujan Legend (Series) (Selite) -ruutuun, niin tuloksena on ryhmitelty pylväskaavio, jossa on erikseen arvosarja miehille ja naisille. Jos kaaviossa ei ole selitettä (Legend), joka selittää värien merkityksen, niin se kannattaa lisätä.

Kun kaavio on valittuna, niin käytettävissä on Design (Rakenne) -välilehti. Kokeile Design-välilehden Switch Row/Column (Vaihda rivi tai sarake) -toimintoa. Seuraa muutoksia kenttäluettelossa, pivot-kaaviossa ja pivot-taulukossa niin opit ymmärtämään kaavion ja taulukon rakennetta.

Prosentteja lukumäärien sijasta

Jos haluan esittää lukumäärät prosentteina, niin napsautan oikean reunan kenttäluettelon Values-ruudun palikkaa ja valitsen esiin tulevasta valikosta Value Field Settings. Value Field Settings -ikkunasta valitsen Show Values As (Näytä arvot muodossa) -välilehden ja valitsen pudotusvalikosta esitystavaksi % of Column Total (Prosenttia sarakkeen summasta).

Pylväiden järjestys

Excel järjestää pivot-taulukon rivit ja pivot-kaavion pylväät luokkien mukaiseen numero/aakkosjärjestykseen. Voin vaihtaa järjestyksen pivot-taulukon Row Labels -pudotusvalikosta tai pivot-kaaviossa olevan painikkeen pudotusvalikosta (painike on näkyvillä, jollet ole piilottanut sitä Analyze – Field Buttons – Hide All -toiminnolla). Pudotusvalikon More Sort Options (Lisää lajitteluvaihtoehtoja) -valinnalla löydät tarjolla olevat vaihtoehdot:

• Voit järjestää luokkien mukaiseen nousevaan tai laskevaan numero/aakkosjärjestyskeen.
• Voit järjestää lukumäärien/prosenttien mukaiseen järjestykseen (eli pylväiden pituuden mukaiseen järjestykseen).

Jos haluat muunlaisen järjestyksen, niin voit siirtää hiirellä pivot-taulukon riviotsikoita riviltä toiselle. Jos esimerkiksi laadin pivot-kaavion koulutus-muuttujasta, niin luokkien mukainen numero/aakkkosjärjestys ei ole toivottu:

Valitsen pivot-taulukosta solun, jossa on teksti Peruskoulu ja raahaan solun reunasta kiinni pitäen ensimmäiseksi, jonka jälkeen koulutukset ovat koulutuksen pituuden mukaisessa järjestyksessä.

Puuttuvat havainnot (blank)

Jos käytän koulutus-muuttujaa Values-ruudussa, niin pivot-taulukon ja pivot-kaavion (blank) viittaa puuttuviin havaintoihin. Puuttuvien havaintojen lukumäärä ei kuitenkaan ole näkyvillä.

Selitys: Excel laskee kuinka monta havaintoarvoa on koulutus-sarakkeen niissä soluissa, joista koulutus puuttuu. Vastaus on tietenkin: ei yhtään.

Ratkaisu: Käytän Values-ruudussa koulutus-muuttujan sijasta nro-muuttujaa (laskentatavaksi täytyy muuttaa sum sijasta count), jolla on havainto jokaisella rivillä.

Jos aineistossa ei ole valmiiksi juoksevaa numerointia, niin sellainen kannattaa lisätä. Tätä juoksevaa numerointia kannattaa käyttää pivot-kaavioiden Values-ruudussa jos olet laskemassa lukumääriä tai lukumääriin pohjautuvia prosentteja. Näin saan tietää myös puuttuvien havaintojen lukumäärän.

Seuraavaksi

Lue myös pivot-kaavioista kirjoittamani jatkoartikkelit:

• Monivalinta pivot-kaaviona
• Määrälliset muuttujat pivot-kaaviona

Spearmanin järjestyskorrelaatio

Päivitetty 19.4.2019.

Järjestysasteikollisille muuttujille korrelaationa käytetään nimenomaan Spearmanin järjestyskorrelaatiota. Ennen Spearmanin järjestyskorrelaation laskemista muuttujien arvot täytyy muuntaa sijaluvuiksi.

Jos muuttujien arvot ovat sijalukuja, niin niiden välinen korrelaatiokerroin lasketaan samoin kuin Pearsonin korrelaatiokerroin (lue lisää artikkelista Korrelaatio ja sen merkitsevyys), mutta sitä kutsutaan Spearmanin järjestyskorrelaatiokertoimeksi.

• Positiivinen järjestyskorrelaatiokerroin merkitsee sitä, että järjestykset ovat jossain määrin samansuuntaiset. Järjestyskorrelaatiokerroin 1 tarkoittaa sijalukujen täsmälleen samaa järjestystä.
• Negatiivinen järjestyskorrelaatiokerroin merkitsee sitä, että järjestykset ovat jossain määrin vastakkaiset. Järjestyskorrelaatio -1 tarkoittaa sijalukujen täsmälleen vastakkaista järjestystä.

Järjestysasteikollisille muuttujille korrelaationa käytetään nimenomaan Spearmanin järjestyskorrelaatiota. Ennen Spearmanin järjestyskorrelaation laskemista muuttujien arvot täytyy muuntaa sijaluvuiksi.

Sijaluvut

Excelissä voin laskea sijaluvut funktiolla RANK.AVG (ARVON.MUKAAN.KESKIARVO). Funktiolle annan kolme argumenttia:

1. Viittaus muuttujan arvoon, jota vastaavan sijaluvun haluan laskea
2. Viittaus kaikkiin muuttujan arvoihin. Viittaus pitää kiinnittää (F4), jos kopioin funktiota muihin soluihin.
3. Kolmanneksi argumentiksi annan 1, jos haluan pienimmälle muuttujan arvolle pienimmän sijaluvun tai 0 jos haluan suurimmalle muuttujan arvolle pienimmän sijaluvun. Tällä ei ole vaikutusta Spearmanin järjestyskorrelaation arvoon.

Jos sama arvo esiintyy useasti, niin sijaluvuksi tulee sijalukujen keskiarvo. Seuraavassa taulukossa arvo 7 esiintyy sijaluvuilla 5, 6 ja 7. Jaetuksi sijaluvuksi tulee sijalukujen keskiarvo (5+6+7)/3=6.

Sijalukujen laskeminen onnistuu vaikka arvot eivät olisikaan suuruusjärjestyksessä.

Korrelaatio

Sen jälkeen kun olen laskenut muuttujan arvoille sijaluvut, voin laskea sijalukujen välisen korrelaation CORREL (KORRELAATIO) -funktiolla. Funktion ensimmäiseksi argumentiksi annan viittauksen ensimmäisen muuttujan sijalukuihin ja toiseksi argumentiksi viittauksen toisen muuttujan sijalukuihin.

Korrelaation merkitsevyys

Jos aineisto pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Järjestyskorrelaation tapauksessa tämä tarkoittaa sijalukujen välisen korrelaation yleistämistä perusjoukkoon.

Pienet korrelaatiot voin selittää otantavirheellä. Otoksessa havaitun korrelaation täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Suuruutta testaan vertaamalla korrelaatiokerrointa hypoteettiseen tilanteeseen, jossa ei ole lainkaan korrelaatiota (korrelaatiokerroin on 0). Jos otoksesta laskettu korrelaatiokerroin poikkeaa riittävästi nollasta, niin voin kutsua korrelaatiota tilastollisesti merkitseväksi.

Korrelaatiokertoimen merkitsevyyden testaamiseksi lasketaan niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: kuinka todennäköistä on saada havaitun suuruinen tai vielä kauempana nollasta oleva korrelaatiokertoimen arvo ilman että korrelaatiota on perusjoukossa? Mitä pienempi p-arvo on sitä enemmän korrelaation yleistäminen perusjoukkoon saa tukea.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Jos haluat tietää p-arvon laskentaperusteesta, niin lue artikkeli Korrelaatio – lisätietoa.

Voit käyttää p-arvon laskemiseen valmista laskentapohjaa testaa_korrelaatio.xlsx. Kirjoita laskentapohjaan otoskoko ja korrelaatiokerroin, jonka jälkeen voit lukea p-arvon. Käytä 2-suuntaista p-arvoa, jos testaat sitä onko korrelaatio nollasta poikkeava. Käytä 1-suuntaista p-arvoa, jos testaat pelkästään korrelaation positiivisuutta tai pelkästään korrelaation negatiivisuutta. Huomaa, että laskentapohjassa on erillinen taulukko pieniä otoskokoja (alle 30) varten.

SPSS

SPSS:llä on helpompaa laskea Spearmanin järjestyskorrelaatiot, koska SPSS määrittää sijaluvut automaattisesti, kun määrität laskettavaksi Spearmanin järjestyskorrelaatiokertoimen. SPSS laskee automaattisesti myös p-arvon ja huomioi pieniin otoksiin liittyvän poikkeavan laskentatavan. Lue lisää SPSS-monisteesta.

Logistinen regressio 2

Päivitetty 5.6.2014

Tämä artikkeli on jatkoa artikkeliin Logistinen regressio.

Askeltava (Stepwise) menetelmä

Selittäviä muuttujia ei pidä ottaa logistiseen regressiomalliin enempää kuin on tarpeellista. Paras tilanne on, jos tiedän mukaan otettavat selittävät muuttujat aiempien aineistojen tai teorian kautta. Jos aiempaa tietoa tai teoriaa ei ole, niin voin käyttää apuna askeltavaa (Stepwise) menetelmää.

SPSS tarjoaa askellukseen Forward– ja Backward-menetelmiä.

Forward-menetelmässä SPSS aloittaa mallista, joka sisältää pelkästään vakiotermin. SPSS lisää malliin selittäviä muuttujia yksi kerrallaan. Lisättävä muuttuja on se, joka lisää eniten mallin selitysvoimaa. Uuden muuttujan lisäämisen jälkeen SPSS tarkistaa, pitäisikö jokin malliin jo lisätyistä muuttujista poistaa. Forward LR -menetelmässä poistamisen kriteerinä käytetään log-likelihoodia. Jos muuttujan poistaminen ei muuta merkitsevästi mallin log-likelihoodia, niin SPSS poistaa muuttujan mallista. Muuttujien lisääminen lopetetaan, kun mikään uusi muuttuja ei enää merkittävästi paranna mallin selitysvoimaa.

Backward-menetelmässä otetaan ensimmäiseen malliin mukaan kaikki ehdokkaat. Tämän jälkeen selittäviä muuttujia poistetaan mallista yksi kerrallaan. Backward LR -menetelmässä poistamisen kriteerinä käytetään log-likelihoodia. Jos muuttujan poistaminen ei muuta merkitsevästi mallin log-likelihoodia, niin SPSS poistaa muuttujan mallista. Muuttujien poistaminen lopetetaan, kun minkä tahansa muuttujan poistaminen heikentää merkittävästi mallin selitysvoimaa.

Käytännössä Forward– ja Backward-menetelmien tuottamat mallit usein poikkeavat toisistaan. Menetelmän ja lopullisen mallin valinnassa kannattaa käyttää tapauskohtaista harkintaa.

Esimerkki

Käytän seuraavassa SPSS-muotoista aineistoa logit2.sav. Aineiston lähde ja tarkempi kuvaus: http://logisticregressionanalysis.com/303-what-a-logistic-regression-data-set-looks-like-an-example/

Suoritan laskennan SPSS:llä:

• Valitsen Analyze – Regression – Binary Logistic.
• Siirrän selitettävän muuttujan Dependent-ruutuun.
• Siirrän selittävät muuttujat Covariates-ruutuun.
• Valitsen Method-alasvetovalikosta menetelmän; tässä esimerkissä Forward LR.
• Valitsen OK.

SPSS:n tulosteissa otsikon Block 0 alla on tiedot mallista, jossa on mukana pelkästään vakiotermi. Askeltavan menetelmän vaiheet ja lopullisen mallin löydän otsikon Block 1 alta.

Omnibus-taulukon Model-rivin Chi-square-sarake kertoo kuinka paljon -2 Log likelihood (-2 Log likelihoodista lisää artikkelissa Log likelihood) on muuttunut verrattuna edeltävään malliin. Tämä muutos noudattaa khiin neliö -jakaumaa, jonka perusteella saadaan muutoksen merkitsevyys (Sig.). Esimerkissämme jokainen malliin lisätyistä viidestä selittävästä muuttujasta on parantanut mallia merkitsevästi (Sig.<0,001).

Variables in the Equation -taulukosta näen malliin lisätyt muuttujat.

Osa aineistosta testiaineistona

Data mining -tyyppisessä analyysissä analysoidaan usein isoja aineistoja. Ison aineiston tapauksessa mallin sopivuutta voidaan testata laskemalla malli osalle aineistosta ja testaamalla kuinka hyvin malli sopii lopulle aineistolle. Tätä varten voin lisätä SPSS-aineistoon ylimääräisen muuttujan, joka erottelee aineiston kahteen osaan:

• osa, jonka perusteella lasketaan malli
• osa, jolla testataan lasketun mallin sopivuutta.

Voin lisätä ylimääräisen muuttujan SPSS:n Transform – Compute Variable -toiminnolla:

• Valitsen Transform – Compute Variable.
• Kirjoitan uudelle muuttujalle nimen Target Variable -ruutuun.
• Kirjoitan Numeric Expression -ruutuun funktion RV.BERNOULLI(0.5).
• Valitsen OK.

Näin laskettu uusi muuttuja saa satunnaisesti arvoja 0 ja 1 siten, että puolet on nollia ja puolet ykkösiä. Voin lisätä tämän muuttujan Logistic Regression -määrittelyikkunassa Selection Variable -ruutuun (olen antanut muuttujalle nimeksi Random). SPSS:lle täytyy kertoa Rule-painikkeella, mille muuttujan arvoille lasketaan logistinen regressio. Seuraavassa olen laskemassa logistista regressiota niiden rivien pohjalta, joissa Random-muuttujan arvo on 1.

Tulosteiden joukossa on muiden muassa Classification Table, josta näen kuinka hyvin malli ennustaa Buy-muuttujan arvoja. Lopullisessa mallissa (Step 4) malli ennustaa ostaneista (Buy=1) 75 % oikein. Aineiston toisessa puolikkaassa malli ennustaa ostaneista (Buy=1) 80,5 % oikein. Ainakin tässä mielessä malli näyttäisi toimivan hyvin.

Jos kokeilet yllä kuvattua esimerkkiaineistolla, niin voit hyvinkin päätyä erilaiseen malliin, koska aineisto voi olla eri tavalla jaettu kahteen osaan.

Kaiken kaikkiaan on kiusallista ja hämmentävää, koska samalla aineistolla voin päätyä eri menetelmillä erilaisiin malleihin. Mallin valinnassa täytyy käyttää tilannekohtaista harkintaa.

 

Logistinen regressio

Päivitetty 5.6.2014

Mistä on kyse?

Esimerkki. Lomaosakkeita myyvä yritys tarjoaa huippuhalvan viikonlopun kylpylässä lomaosakkeen esittelyyn osallistuville. Tarjous kannattaa kohdistaa henkilöille, joiden todennäköisyys lomaosakkeen ostoon on tavanomaista suurempi. Aiempien esittelyiden ja toteutuneiden kauppojen perusteella voidaan laatia malli, jolla lasketaan taustatietojen perusteella henkilön todennäköisyys lomaosakkeen ostoon.

Esimerkki. Luottoriskin arvioimiseksi pankin on hyvä tietää kuinka todennäköisesti luotonottajalle tulee maksuhäiriöitä. Aiempien maksuhäiriöiden perusteella voidaan laatia malli, jolla lasketaan taustatietojen perusteella luotonottajan todennäköisyys maksuhäiriöille.

Esimerkki. Lääkäri diagnosoi sairauden. Aiempien potilaiden potilastietojen perusteella voidaan laatia malli, jolla lasketaan potilaan parantumisen todennäköisyys.

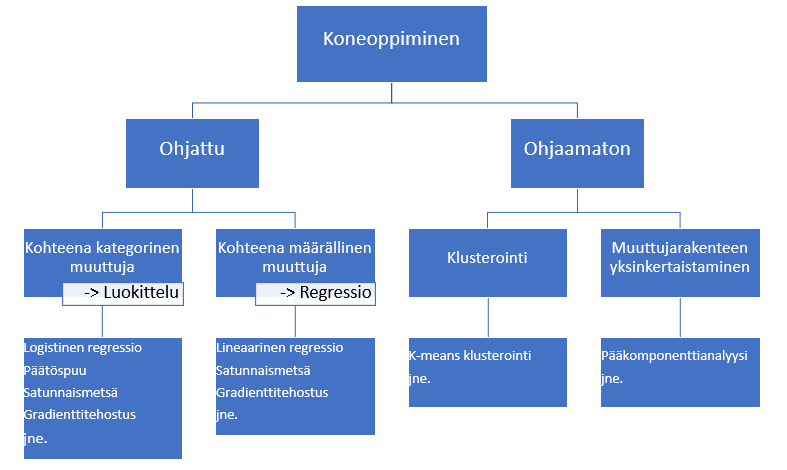
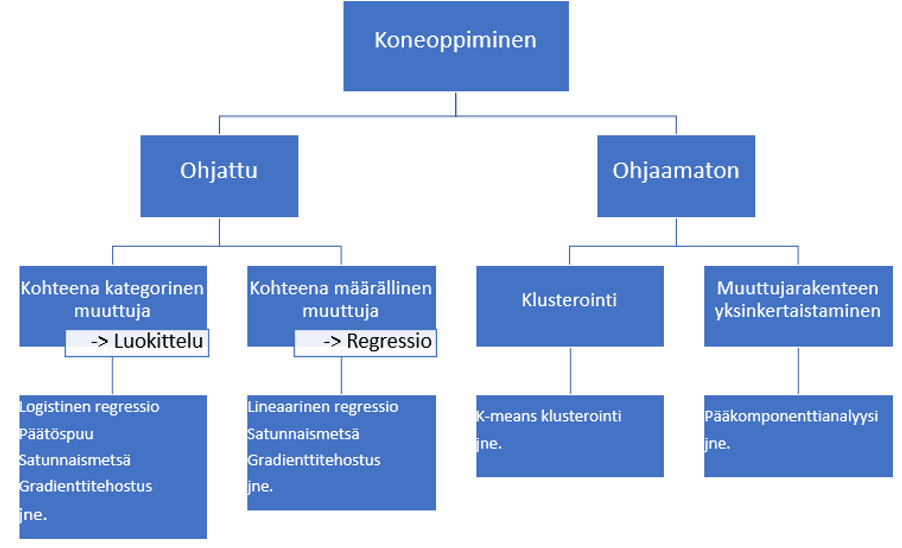
Edellä kuvatuissa esimerkeissä voidaan käyttää todennäköisyyden arviointiin logistista regressiota. Logistista regressiota voidaan käyttää, jos ennustettavana on kategorinen muuttuja: ostaa tai ei osta, tulee maksuhäiriöitä tai ei tule, paranee tai ei parane. Selittävinä muuttujina voi olla sekä määrällisiä että kategorisia muuttujia.

Ilman käsitteiden odds ja logit ymmärtämistä logistista regressiota ei voi ymmärtää, joten aloitan niistä.

Odds

Odds-käsitteelle ei valitettavasti ole vakiintunutta suomennosta. Monet sanakirjat antavat suomennokseksi todennäköisyys, mutta odds on tarkkaan ottaen todennäköisyyksien suhde. Suomennoksia veto, vedonlyöntisuhde ja riski näkyy käytettävän. Minä käytän seuraavassa sekaannuksien välttämiseksi englanninkielistä termiä odds.

Jos tapahtuman todennäköisyys on p, niin odds tapahtuman puolesta:

odds = p / (1-p)

Jos odds on tiedossa, niin yllä olevasta kaavasta voin ratkaista todennäköisyyden:

p = odds / (odds+1)

Esimerkki. Nopanheitossa todennäköisyys saadaa kuutonen on yksi kuudesta (1/6) ja todennäköisyys olla saamatta kuutosta on viisi kuudesta (5/6). Odds on todennäköisyyksien suhde:

• Odds kuutosen puolesta = (1/6)/(5/6)=1/5=0,2
• Odds kuutosta vastaan = (5/6)/(1/6)=5

Logit

Edellisen nopanheittoesimerkin odds 0,2 kuutosen puolesta ja 5 kuutosta vastaan kuvaavat samaa tilannetta eri näkökulmista. Tämä ilmenee jännästi, jos otan logaritmit:

• ln(0,2) ≈ -1,609
• ln(5) ≈ 1,609

Jatketaan nopanheitolla ja tarkastellaan todennäköisyyttä saada parillinen silmäluku. Todennäköisyys on 1/2 ja odds on (1/2)/(1/2)=1. Tässä tapauksessa logaritmi on ln(1)=0.

ln(odds) on niin hyödyllinen, että sille on annettu oma nimi logit:

logit = ln (odds)

Logitilla on muiden muassa seuraavat ominaisuudet:

• Jos todennäköisyys on 50 %, niin logit = 0.
• Jos todennäköisyys on alle 50 %, logit on negatiivinen. Logit on sitä enemmän negatiivinen mitä pienempi todennäköisyys.
• Jos todennäköisyys on yli 50 %, niin logit on positiivinen. Logit on sitä enemmän positiivinen mitä isompi todennäköisyys.

Jatkoa ajatellen on hyvä oppia miten logitista päästään takaisin oddsiin. Tässä tarvitaan luonnollisen logaritmin käänteistoimitusta (e on luonnollisen logaritmin kantaluku eli Neperin luku):

odds=e^ln(odds)=e^logit

Edellä jo totesin, että oddsista saadaa todennäköisyys laskemalla odds/(odds+1). Yhdistämällä tämä tulos äskeiseen, saadaan muunnoskaava logitista todennäköisyyteen:

p = e^logit/(1+e^logit)

Logistinen regressio

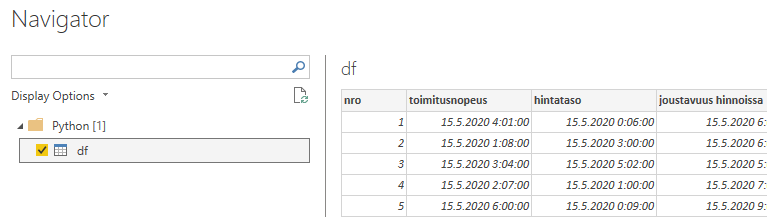
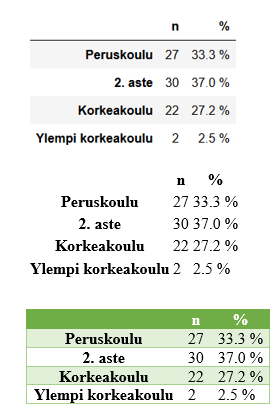
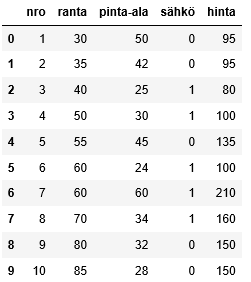
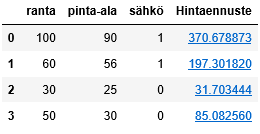
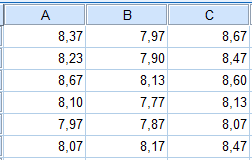
Seuraavassa esimerkkinä käytettävä aineisto SPSS-muodossa logit1.sav (aukeaa vain SPSS:llä) ja Excel-muodossa logit1.xlsx. Kiinnostuksen kohteena on Buy (1=osti, 2=ei ostanut). Seuraavassa on näkyvillä aineiston ensimmäiset rivit:

Selittävinä muuttujina ovat income (tulot), isfemale (1=nainen, 0=mies) ja ismarried (1=naimisissa, 0=naimaton). Otetaan tavoitteeksi laatia malli, jonka avulla voidaan ennustaa oston todennäköisyys muuttujien income, isfemale ja ismarried perusteella.

Logistinen regressiomalli on lineaarinen regressiomalli, jossa selitettävänä muuttujana on logit (todennäköisyyttä ei sellaisenaan saada sovitettua lineaariseen malliin). Esimerkkiaineiston tapauksessa pyrimme muodostamaan mallin

logit = b0+b1*income + b2*isfemale + b3*ismarried

Mallin parametrit (b0, b1, b2, b3) määritetään maximum likelihood eli suurimman uskottavuuden -menetelmällä. Mallin käyttäjän ei välttämättä tarvitse ymmärtää maximum likelihood -menetelmän yksityiskohtia, mutta seuraavat perusideat on hyvä tuntea:

• Parametreille annetaan arvauksena alkuarvot.
• Lasketaan todennäköisyys sille, että havaittu data saataisiin näillä parametrien arvoilla.
• Korjataan parametreja siten että päästään parempaan tulokseen.
• Korjauksia tehdään, kunnes päästään parhaaseen mahdolliseen tulokseen. Paras mahdollinen tulos on se, johon liittyy suurin mahdollinen todennäköisyys sille, että havaittu data saataisiin valituilla parametrien arvoilla.

Esimerkkiaineisto maximum likelihood -menetelmä antaa malliksi:

logit = -12,033 + 0,00016742*income + 1,3653*isfemale + 1,3804*ismarried

Esimerkiksi 50000 ansaitsevan naimattoman naisen logit:

logit = -12,033 + 0,00016742*50000+1,3653*1+1,3804*0 ≈ -2,2967

Edellä jo opimme, että logit voidaan muuntaa todennäköisyydeksi p = e^logit/(1+e^logit). Näin esimerkiksi 50000 ansaitsevan naimattoman naisen todennäköisyys ostolle:

p = e^-2,2967/(1+e^-2,2967) ≈ 0,09 = 9 %

SPSS ja logistinen regressio

Voin suorittaa laskennan SPSS:llä seuraavasti:

• Valitsen Analyze – Regression – Binary Logistic.
• Siirrän selitettävän muuttujan Dependent-ruutuun.
• Siirrän selittävät muuttujat Covariates-ruutuun.

SPSS:n tulosteissa on kaksi mallia. Otsikon Block 0 alta löydän tiedot mallista, jossa on ainoastaan vakiotermi b0, mutta ei lainkaan selittäviä muuttujia. Tämä malli on mukana vertailun vuoksi.

Tulosteesta voin lukea, että vakiotermi on -1,478. Tämä tarkoittaa mallia logit=-1,478. Tällöin todennäköisyys p = e^-1,478/(1+e^-1,478) ≈ 0,1857. Tämä on sama kuin aineistossa niiden osuus, jotka ovat ostaneet (125/673≈0,1857). Pelkästään vakiotermin sisältävä malli siis antaa ostamisen todennäköisyydeksi ostaneiden osuuden. Koska ostaneiden osuus on alle 50 %, niin mallin mukaan ennuste on aina ”ei osta”. Tällainen ennuste osuu kohdalleen 81,4 prosentissa tapauksista (548/673≈0,814).

Varsinaisen selittäviä muuttujia sisältävän mallin tiedot löydän otsikon Block 1 alta. Ensiksi arvioin mallin hyvyyttä verrattuna malliin, jossa on vain vaikiotermi. Hyvyyttä voin arvioida Omnibus-taulukon Model-riviltä. Chi-square-sarake kertoo kuinka paljon -2 Log likelihood (-2 Log likelihoodista lisää artikkelissa Log likelihood) on muuttunut verrattuna pelkästään vakiotermin sisältävään malliin. Tämä muutos noudattaa khiin neliö -jakaumaa, jonka perusteella saadaan muutoksen merkitsevyys (Sig.). Esimerkissämme selittävät muuttujat sisältävä malli on merkitsevästi parempi (Sig.<0,001) kuin pelkästään vakiotermin sisältävä malli.

Model Summary -taulukosta löydän -2 Log likelihood -arvon lisäksi kaksi R²-arvoa (lisätietoa artikkelissa Log likelihood), jotka yrittävät jäljitellä lineaarisen regressiomallin selityskerrointa. Näiden lisäksi on esitetty monia muita tapoja laskea R²-arvo. Yksimielisyyttä parhaasta laskentatavasta ei ole, minkä vuoksi R²-arvojen käyttö ja tulkinta on hankalaa. Aina kuitenkin pätee seuraava: mitä lähempänä R²-arvo on ykköstä sitä parempi.

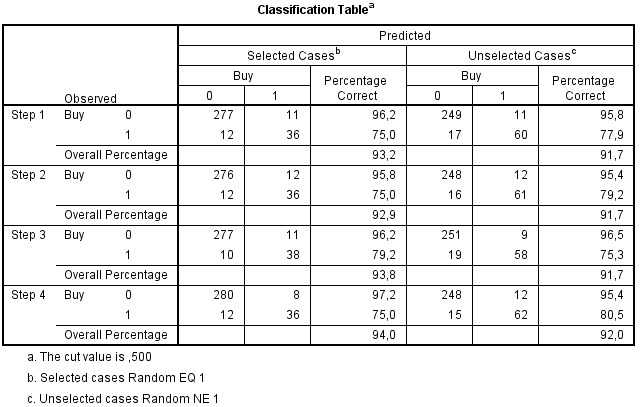
Classification-taulukosta selviää, että malli ennustaa 95,8 % ei ostaneista oikein ja 84,8 % ostaneista oikein. Tässä mielessä malli vaikuttaa onnistuneelta.

Variables in the Equation -taulukko sisältää regressiokertoimet. Income-kerroin (B) ,000 ei tarkoita, että tuloilla ei olisi mitään vaikutusta ostamiseen. Jos lisään desimaalien määrää kyseisessä solussa, niin huomaan kertoimen poikkeavan nollasta.

Varmistan aina, että regressiokertoimet poikkeavat merkitsevästi nollasta. Tämä selviää Wald’in testimuuttujan avulla. Wald’in testimuuttuja saadaan jakamalla kerroin B keskivirheellään S.E. ja korottamalla tulos toiseen potenssiin. Wald’in testimuuttujan tiedetään noudattavan khiin neliö -jakaumaa, jonka perusteella merkitsevyys (Sig.) voidaan laskea. Esimerkissämme kaikki kertoimet poikkeavat merkitsevästi nollasta (Sig.<0,001), joten kaikki selittävät muuttujat voidaan tämän perusteella pitää mallissa mukana.

Malli on siis esimerkkimme tapauksessa (olen ottanut desimaaleja hieman enemmän Variables in the Equation -taulukossa oli näkyvillä):

logit = -12,033 + 0,00016742* income + 1,3653*isfemale + 1,3804*ismarried

Mallin parametrit (kertoimet) voidaan tulkita kuten lineaarisessa mallissa yleensäkin. Esimerkiksi income-kerroin 0,00016742 kertoo, että yhden euron lisäys tuloihin merkitsee 0,00016742 kasvua logitissa. Tämä ei kuitenkaan ole kovinkaan käyttökelpoinen tieto, koska logit on hieman hankala käsite ymmärrettäväksi.

Variables in the Equation -taulukossa on hieman helpommin tulkittavat muunnetut kertoimet Exp(B)-sarakkeessa. Exp(B)-sarakkeen kertoimet kertovat kuinka moninkertaisksi odds muuttuu, kun selittävä muuttuja kasvaa yhdellä yksiköllä.

• Jos tulot kasvat yhdellä eurolla, niin odds kasvaa 1,0001674 kertaiseksi.
• Naisilla odds on 3,917-kertainen miehiin verrattuna.
• Naimisissa olevilla odds on 3,976-kertainen naimattomiin verrattuna.

Selittävien muuttujien valinta

Oma kysymyksensä on selittävien muuttujien valinta, jos ehdolla on paljon mahdollisia selittäviä muuttujia. Tästä lisää artikkelissa Logistinen regressio 2.

Log-likelihood

Päivitetty 27.7.2020

Tämä artikkeli täydentää artikkelia Logistinen regressio.

Logistisen regressiomallin laskenta ja sopivuuden arviointi perustuu log-likelihood -lukuun. Yritän tässä artikkelissa valottaa log-likelihood -luvun taustaa ja laskentaa.

Suurimman uskottavuuden menetelmä ja likelihood

Logistisen regressiomallin parametrit/kertoimet määritetään maximum likelihood eli suurimman uskottavuuden menetelmällä:

• Parametreille annetaan arvauksena alkuarvot.
• Lasketaan todennäköisyys (likelihood) sille, että havaittu data saataisiin näillä parametrien arvoilla.
• Korjataan parametreja siten että päästään parempaan tulokseen (suurempi likelihood).
• Korjauksia tehdään, kunnes päästään parhaaseen mahdolliseen tulokseen. Paras mahdollinen tulos on se, johon liittyy suurin mahdollinen todennäköisyys (maximum likelihood) sille, että havaittu data saataisiin valituilla parametreilla.

Likelihood’in laskenta

Käytän seuraavassa esimerkissä Excel-aineistoa logit1.xlsx, jonka alkuosan näet seuraavassa:

Artikkelissa Logistinen regressio olen esittänyt, miten tälle aineistolle lasketaan logistinen regressiomalli SPSS:llä. Esitän seuraavassa, miten likelihood ja log-likelihood lasketaan SPSS:n laskemalle regressiomallille. Laskennan olen suorittanut Excel-taulukkoon käyttäen SPSS:n antamia mallin parametreja, jotka olen kopioinut Exceliin. Excel käyttää koko ajan laskennassa 15 merkitsevän numeron tarkkuutta. Seuraavassa esittämäni laskelmat näyttävät vain pyöristettyjä likiarvoja.

Ensimmäisen vastaajan logit tulee suoraan regressiomallin yhtälöstä:

logit = -12,033 + 0,00016742*24000+1,3653*1+1,3804*0 ≈ -6,649

Logitista saadaan odds=e^logit=e^-6,649≈0,00129493

Ostamisen todennäköisyys on probability=odds/(1+odds)≈0,00129326

Likelihood on ostamisen todennäköisyys, jos kyseinen vastaaja on ostanut. Muussa tapauksessa likelihood saadaan vähentämällä ostamisen todennäköisyys ykkösestä. Ensimmäisen vastaajan tapauksessa

likelihood≈1-0,00129326≈0,99870674

Todennäköisyys, että kaikki havainnot ennustetaan oikein saadaan (todennäköisyyksien kertolaskusääntö) kertomalla likelihood’it keskenään. Isompien aineistojen tapauksessa tällainen kertolasku ei onnistu edes tietokoneelta. Niinpä onkin matemaattisesti mielekästä siirtyä tarkastelemaan likelihood’in logaritmia. Logaritmien käyttö mahdollistaa kertolaskun korvaamisen yhteenlaskulla, koska logaritmien laskusääntöjen mukaan tulon logaritmi saadaan logaritmien summana. Näin päästään log-likelihood -lukuun.

log-likelihood≈ln(0,99870674)≈-0,001294096

Muiden vastaajien log-likelihood lasketaan samalla periaatteella.

Likelihood on todennäköisyys, joten se saa arvoja väliltä [0,1]. Tästä seuraa, että log-likelihood saa negatiivisia arvoja tai arvon 0, jos likelihood=1. Mitä lähempänä nollaa log-likelihood on, sitä sopivampi malli.

SPSS:n ja myös muiden tilasto-ohjelmien tulosteissa ilmoitetaan log-likelihood kerrottuna luvulla -2. Tätä merkitään usein -2LL. Mitä pienempi -2LL on, sitä sopivampi malli on kyseessä.

Luvulla -2 kertominen tehdään, koska näin saadaan arvo, jonka muutoksen (verrattuna toiseen malliin) tiedetään noudattavan khiin neliö -jakaumaa. Khiin neliö -jakaumasta saadaan merkitsevyystaso (Sig.), jonka avulla voidaan arvioida mallin paremmuutta toiseen malliin verrattuna. Yleensä mallia pidetään merkitsevästi toista mallia parempana, jos Sig.<0,05.

Pseudo-selityskerroin

Logistisen regressiomallin selityskertoimen (R²) laskemiseksi on esitetty useita vaihtoehtoisia tapoja. Useimpien tapojen perustana on likelihood. Selityskertoimet eivät ole tulkinnallisesti yhtä konkreettisia kuin lineaarisen regression selityskerroin, joka ilmaisee kuinka suuren osan selitettävän muuttujan valihtelusta malli selittää. Logistisen regressiomallin selityskertoimia onkin tapana kutsua pseudo-selityskertoimiksi. SPSS esittää tulosteissaan Cox & Snell ja Nagelkerke -selityskertoimet:

Cox & Snell – selityskertoimen ongelma on, että se ei voi koskaan saavuttaa arvoa 1. Nagelkerke -selityskerroin on Cox & Snell -kertoimen korjattu versio, joka laajentaa mahdollisen arvoalueen arvoon 1 asti. Kertoimien arvoille ei ole mitään täsmällistä tulkintaa. Kuitenkin aina pätee: mitä lähempänä R²-arvo on ykköstä sitä parempi.

Sparkline-kaaviot

Päivitetty 2.2.2019

• sparklin.xlsx

Hyvin laaditusta taulukosta on helppo tarkastella yksittäisiä numeroita. Tämän lisäksi usein on tarpeen saada kokonaisnäkemys numeroiden kehityssuunasta tai jakaumasta. Sparklines-kaaviot ovat helppo ja nopea tapa kokonaisnäkemyksen muodostamiseen.

Seuraavaan taulukkoon on kirjattu myynnin määrät miljoonina euroina neljällä eri alueella vuosineljänneksittäin. Taulukon viereen lisätyt sparkline-viivat näyttävät myynnin kehityksen kullakin alueella. Taulukon alapuolelle lisätyt sparkline-pylväät näyttävät myynnin alueittaisen jakauman kullakin vuosineljänneksellä.

Voin lisätä Sparkline-kaavioita seuraavasti:

• Valitsen solut, joihin haluan Sparkline-kaaviot.
• Valitsen Insert (Lisää) -välilehdeltä Sparkline-kaavion.
• Määritysikkunassa määritän, mistä arvoalueesta luon Sparkline-kaaviot.
• OK.

Kun napsautan Sparkline-kaavioita, niin kaikki samalla kertaa luodut Sparkline-kaaviot tulevat valituiksi. Voin säätää valittuja kaavioita Design (Rakenne) -välilehdellä. Erityisesti tarkistan Axis (Akseli) -asetukset. Edellä olleessa esimerkissä olen säätänyt pylväiden pystyakselin pienimmäksi arvoksi 0 ja suurimman arvon samaksi kaikissa kaavioissa. Edellä olleessa esimerkissä en ole yhdenmukaistanut Sparkline-viivojen pystyakselia. Tällöin en voi vertailla Sparkline-viivoista myynnin määriä eri alueilla. Sen sijaan näen selkeästi myynnin kehityksen kullakin alueella.

Kannattaa tutustua ja kokeilla myös muihin Design (Rakenne) -välilehden asetuksiin.

Opi lisää Excel-esimerkeistä sparklin.xlsx.

Taulukoita ja pylväitä

Päivitetty 2.2.2019

• taulpylv.xlsx

Nykyaikainen yhteiskunta pyörii numeroiden ympärillä. Päätöksiä tehdään numeroiden pohjalta. Ei ole yhdentekevää, mistä numerot tulevat? Luotettavasta lähteestä asianmukaisia menetelmiä käyttäen tuotetut numerot ovat painavampia kuin epämääräisestä lähteestä peräisin olevat numerot. Useimmat päätöksenteossa käytettävät numerot ovat tiedon keräämisen ja jalostamisen tuloksia.

Tiedon kerääminen

Tietoa kerätään muiden muassa seuraavilla tavoilla:

• Yritysten tietokantoihin tietoa kerääntyy päivittäisten toimintojen seurauksena (myyntitietoja, laskutustietoja, asiakaspalautteita, yrityksen nettisivujen käyttäjätilastoja jne.)
• Monien laitosten ja instituutioiden tehtäviin kuuluu tietojen kerääminen (Tilastokeskus, Suomen Pankki, ETLA jne.)
• Ihmisten mielipiteitä (asiakastyytyväisyydestä, ostoaikeista, työtyytyväisyydestä jne.) kerätään kyselylomakkeilla.

On tärkeää, että tiedon lähde ja keruutapa on hyvin dokumentoitu. Näin voidaan arvioida kerätyn tiedon luotettavuutta.

Tiedon jalostaminen

Kerätyt tiedot ovat harvoin sellaisenaan käyttökelpoisia päätöksenteossa. Tiedoista jalostetaan yhteenvetoja ja analyyseja, joista saadaan päätöksenteossa hyödynnettäviä numeroita.

On tärkeää, että yhteenvetojen ja analyysien laskentamenetelmät ovat hyvin dokumentoitu. Numeroillahan ei ole mitään arvoa, jos niiden luotettavuudesta ei ole takeita.

Taulukoita ja pylväitä

Numerot (lukumäärät, prosentit, eurot, keskiarvot jne.) esitetään yleensä taulukoina. Taulukko on selkeä ja täsmällinen esitystapa, jonka etuja ovat ainakin seuraavat:

• Hyvin laadittu taulukko esittää numerotiedon tarkasti ja täsmällisesti ja täyttää vaativankin lukijan tiedon tarpeen.
• Samassa taulukossa voidaan esittää sekä lukumääriä että prosentteja.
• Samassa taulukossa voidaan esittää useita tunnuslukuja, esimerkiksi keskiarvo, keskihajonta, n-arvo jne.

Taulukon sisältöä voin rikastaa tekemällä vertailuja ja/tai prosentuaalisia vertailuja esimerkiksi koko otokseen, aiempaan ajankohtaan tai toiseen tutkimukseen.

Joissain tapauksissa on hyödyllistä havainnollistaa taulukon sisältöä pylväskuviona. Pylväskuvion etuja ovat ainakin seuraavat:

• Hyvin laadittu kuvio voi antaa yhdellä silmäyksellä havainnollisen yhteenvedon arvojen jakaumasta.
• Numeroihin tottumaton lukija vertailee pylväiden pituuksia helpommin kuin numeroita.

Olen kerännyt sinua varten hyviä ja suositeltavia käytänteitä taulukoiden ja pylväiden käyttöön. Toivottavasti saat Excel-tiedoston taulpylv.xlsx esimerkeistä ideoita ja malleja omiin taulukoihin ja pylväskuvioihin.

Visuaalinen taulukko

Päivitetty 9.4.2021

Tämän artikkelin esimerkkitaulukot vistaul.xlsx

Huomautus: Jos oman organisaatiosi raportointiohje on ristiriidassa tämän artikkelin suositusten kanssa, niin noudata oman organisaatiosi raportointiohjetta.

Numerot pääosassa

Jos tarkoitat taulukon muiden luettavaksi, niin taulukon ulkoasu kannattaa viimeistellä harkiten.

Numerot ovat taulukon varsinainen sisältö. Hyvässä taulukossa numerot ovat pääosassa ja helposti luettavissa. Tasaa luvut solun oikeaan reunaan. Luettavuuden parantamiseksi myös sarakeotsikot kannattaa tasata samalla tavalla solun oikeaan reunaan. Säädä esitettävien lukujen tarkkuus lukijalle sopivaksi:

• Desimaaleja vain sen verran kuin arvelet lukijan tarvitsevan.
• Isot luvut vain sillä tarkkuudella kuin arvelet lukijan tarvitsevan. Jos esität lukuja esimerkiksi miljoonien tarkkuudella, niin voit lyhentää luvut. Tällöin tietenkin ilmoitat sarakeotsikossa tai taulukon otsikossa esitettyjen lukujen yksikön.

Tekstiä tarvitaan otsikoiksi ja selitykseksi sen verran että lukija voi ymmärtää taulukon asiayhteydestään irrotettunakin.

Järjestä ja ryhmittele taulukon tiedot mahdollisimman havainnollisesti. Käytä ryhmittelyn apuna ensisijaisesti tyhjää tilaa. Joissain tapauksissa voit käyttää hillittyä vaakaviivaa. Isojen taulukoiden luettavuutta voit parantaa asettamalla joka toisen rivin taustaväriksi esimerkiksi vaalean harmaan.

Taulukossa 1 on paljon lukuja. Luettavuuden parantamiseksi on käytetty seuraavia keinoja:

• Luvut on lyhennetty miljooniksi euroiksi.
• Lukujen luettavuutta on parannettu tuhat-erottimella (väli kolmen viimeisen  numeron (satojen miljoonien) edessä.
• Otsikot on erotettu muusta tiedosto hillityillä harmailla viivoilla.
• Sarakkeiden väliin on jätetty tyhjää tilaa luettavuuden helpottamiseksi.
• Rivien luettavuutta on helpotettu joka toisen rivin vaalean harmaalla taustalla.
• Yhden rivin kohdalla on jaettu riviotsikko kahdelle riville, koska muutoin taulukko ei olisi mahtunut sivun leveyteen.

Taulukko 1. Yritysten velat, milj. euroa (Lähde: Rahoitustilinpito, Tilastokeskus 2013)

Jos haluat korostaa joitain taulukon osia, niin hillitty taustaväri tai kehys sopii hyvin tarkoitukseen. Myös fontin väriä, lihavointia tai kursivointia voi harkiten käyttää.

Taulukossa 2 lukijan huomio kiinnitetään siihen, että kahden koulutusalan kohdalla uusien opiskelijoiden lukumäärä on pudonnut selvästi.

Taulukko 2. Ammattikorkeakoulujen opiskelijat koulutusalan mukaan 2012-2013 (Lähde: Ammattikorkeakoulutus, Tilastokeskus 2013)

Lähde näkyviin

Jos tieto on peräisin muualta kuin itseltäsi, niin kerro tiedon lähde. Näin on menetelty taulukossa 1 ja taulukossa 2.

Muista n

Jos esität taulukossa prosentteja, niin lukijan täytyy nähdä lukumäärä (n), josta prosentit on laskettu. Jos esität taulukossa keskiarvoja tai muita tunnuslukuja, niin lukijan täytyy nähdä niiden arvojen lukumäärä (n), joiden pohjalta tunnusluku on laskettu.

Taulukossa 3 n nähdään taulukon viimeiseltä riviltä (Vastauksia).

Taulukko 3. Kanta väittämään ’Taustamusiikiksi sopii jazz’ asiakkuuden potentiaalisuuden mukaan

Järjestä

Jos taulukossa esitettävillä asioilla ei ole luontaista järjestystä, niin järjestä numerotiedon mukaiseen järjestykseen (lukumäärän, prosentin, keskiarvon jne. mukaan). Taulukko 4 on järjestetty tyytyväisyyskeskiarvojen mukaiseen järjestykseen.

Taulukko 4. Tyytyväisyyskeskiarvoja, asteikko 1-5 (1=erittäin tyytymätön, 5=erittäin tyytyväinen)

Aiemmin esitetyn taulukon 2 järjestys voi näyttää mielivaltaiselta. Se ei kuitenkaan ole mielivaltainen, vaan on peräisin Opetushallinnon koulutusluokituksesta.

Fontti

Jos taulukko on raportin osana, niin fontin ei tarvitse välttämättä olla sama kuin raportin tekstin fontti. Tärkeintä on, että taulukosta toiseen käytetään samaa fonttia.

Taulukon fonttikoko voi olla sama tai hieman pienempi kuin raportin tekstin fonttikoko. Ison taulukon voi esittää muita taulukoita pienemmällä fontilla, mutta tämä ei ole suotavaa.

Liian iso taulukko

Jos taulukko ei mahdu sivulle, niin mieti

• onko kaikki taulukossa esitettävä välttämätöntä vai voitko karsia jotain pois
• voitko pilkkoa taulukon useammaksi pienemmäksi taulukoksi
• jos kyseessä on aikasarja, niin voitko esittää sen taulukon sijasta viivakaaviona.

Leveyssuunnassa liian ison taulukon voit sijoittaa sivulle pienennettynä. Tämä ei näytä kovin hyvältä ja on vaikeasti luettava erityisesti heikkonäköiselle.

Taulukko 5. Kanta väittämään ’Taustamusiikiksi sopii jazz’ asiakkuuden potentiaalisuuden ja sukupuolen mukaan (taulukko on liian leveä ja sitä on pienennetty)

Joissain tapauksissa leveän taulukon voi luontevasti kaventaa sijoittamalla taulukon osia allekkain. Taulukon 5 sisältö voidaankin esittää taulukkona 6 ilman pienentämistä.

Taulukko 6. Kanta väittämään ’Taustamusiikiksi sopii jazz’ asiakkuuden potentiaalisuuden ja sukupuolen mukaan (parempi esitystapa kuin taulukko 5)

Taulukko vai graafinen esittäminen?

Valitse esitystapa tarkoituksen ja lukijan mukaan.

Taulukon etuja ovat ainakin seuraavat:

• Hyvin laadittu taulukko esittää numerotiedon tarkasti ja täsmällisesti ja täyttää vaativankin lukijan tiedon tarpeen.
• Samassa taulukossa voidaan esittää sekä lukumääriä että prosentteja.
• Samassa taulukossa voidaan esittää useita tunnuslukuja, esimerkiksi keskiarvo, keskihajonta, n-arvo jne.

Graafisen esittämisen etuja ovat ainakin seuraavat:

• Hyvin laadittu kaavio voi antaa yhdellä silmäyksellä havainnollisen yhteenvedon tarkasteltavasta asiasta.
• Numeroihin tottumaton lukija vertailee pylväiden pituuksia helpommin kuin numeroita.
• Ajallista kehitystä on helpompi seurata viivakaaviosta kuin numerotaulukosta.

Usein kysyttyä

Kysymys: Eikö taulukko kannattaisi viivoittaa vaaka- ja pystyviivoin, jotta taulukon tiedot erottuisivat paremmin toisistaan?

Vastaus: Vertaa seuraavia taulukoita:

Viivoitetussa taulukossa katse kiinnittyy helposti viivoitukseen eikä taulukon pääosassa oleviin lukuihin.

Tämän artikkelin esimerkkitaulukot vistaul.xlsx

Ruutu- ja janakaavio

Päivitetty 2.2.2019

• tunnuslukuja.xlsx

Viiden luvun yhteenvedon voin havainnollistaa ruutu- ja janakaavion avulla. Ruutu- ja janakaaviolla on monta nimeä: laatikko- ja viiksikaavio, laatikko- ja viivakaavio, box & whisker -kaavio, boxplot.

Ruutu- ja janakaavion rakenneosat ovat ruutu ja ruudun päistä lähtevät janat:

• Ruudun alareuna vastaa alaneljännestä ja yläreuna yläneljännestä. Ruudun sisään piirretty viiva vastaa mediaania ja rasti keskiarvoa.
• Janojen päät vastaavat pienintä ja suurinta. Jos datassa on niin kutsuttuja poikkeavia arvoja, niin ne esitetään janan ulkopuolisina pisteintä. Poikkeavaksi arvoksi lasketaan arvo, joka on yli 1,5 laatikon korkeuden päässä laatikon reunasta.

Seuraavassa esitän neljän rahastoluokan tuottojen jakaumaa heinäkuussa 2015 (Lähde: Sijoitustutkimus, n vaihtelee välillä 32-58).

Kaikkein pienimmät tuotot ovat kehittyville markkinoille sijoittavissa rahastoissa ja suurimmat Pohjois-Amerikkaan sijoittavissa rahastoissa. Tuotot ovat vaihdelleet eniten Pohjois-Amerkikkaan sijoittavissa rahastoissa. Eurooppaan sijoittavissa rahastoissa tuotoissa ei ole paljoa vaihtelua, mutta huomiota kiinnittää muutama poikkeavan tuoton omaava rahasto sekä ylä- että alapäässä.

Ruutu- ja janakaavio voi epäonnistua, jos et huomioi seuraavia vinkkejä:

VINKKI 1: Jos ryhmittelevän muuttujan arvot ovat datassa numeroita (esimerkiksi 1=mies ja 2=nainen), niin data pitää lajitella (järjestää) ryhmittelevän muuttujan mukaan kaavion onnistumiseksi.

VINKKI 2: Jos ryhmittelevän muuttujan arvot ovat datassa numeroita (esimerkiksi 1=mies ja 2=nainen), niin en valitse ryhmittelevän muuttujan arvoja ennen kaaviolajin valitsemista, vaan teen kaavion aluksi vain muuttujalle, jolle lasken viiden luvun yhteenvedon. Tämän jälkeen valitsen kaavionmuokkaustyökalujen Design (Rakenne) -välilehdeltä Select Data (Valitse tiedot). Select Data -toiminnolla pääsen lisäämään sukupuolet luokka-akselin otsikoiksi (Category Axis Labels).

VINKKI 3: Jos ryhmittelevän muuttujan arvot ovat datassa tarkasteltavan muuttujan oikealla puolella, niin en valitse ryhmittelevän muuttujan arvoja ennen kaaviolajin valitsemista, vaan teen kaavion aluksi vain muuttujalle, jolle lasken viiden luvun yhteenvedon. Tämän jälkeen valitsen kaavionmuokkaustyökalujen Design (Rakenne) -välilehdeltä Select Data (Valitse tiedot). Select Data -toiminnolla pääsen lisäämään ryhmittelevän muuttujan arvot luokka-akselin otsikoiksi (Category Axis Labels).

Lisätietoa

Tämän oppii vain tekemällä itse. Harjoittele työkirjalla tunnuslukuja.xlsx.

Säteittäinen kaavio

Päivitetty 26.3.2013

Oheinen kaavio esittää miesten ja naisten tyytyväisyyskeskiarvoja (tyytyväisyys mitattu asteikolla 1-5; 1=erittäin tyytymätön, 5=erittäin tyytyväinen).

Kaaviosta näen helposti, että naisten tyytyväisyyskeskiarvo on selvästi suurempi johdon, työympäristön ja palkan kohdalla.

Kaaviolajin nimi on Excelissä Radar (Säteittäinen). Äskeisen kaavion loin seuraavan taulukon pohjalta:

Akselin vaihdoin alkamaan nollan sijaan arvosta yksi, koska tyytyväisyysasteikon pienin arvo on yksi. Akselin ominaisuuksiin pääsen napsauttamalla hiiren kakkospainiketta akselin (säteen) päällä ja valitsemalla Format Axis (Muotoile akseli).

Säteittäisessä kaaviossa kullakin luokalla on oma arvoakseli (säde). Äskeisessä kaaviossa luokkia ovat tyytyväisyys johtoon, tyytyväisyys työtovereihin jne. Arvoakselina on tyytyväisyys 1-5. Säteittäinen kaavio soveltuu erityisesti tilanteisiin, joissa vertaillaan kahta arvosarjaa, kuten edellä miesten keskiarvoja ja naisten keskiarvoja.

SPSS: Toistomittausten varianssianalyysi

Päivitetty 25.9.2020

Jos toistomittausten varianssianalyysi en sinulle entuudestaan tuntematon menetelmä, niin kannattaa lukea ensiksi artikkeli Toistomittausten varianssianalyysi.

Esimerkki. Autovalmistaja testaa automallin polttoaineen kulutusta kolmella erilaisella säädöllä (A, B ja C). Kokeessa käytetään kuutta eri kuljettajaa. Jokainen kuljettaja ajaa kerran kullakin säädöllä. Koska järjestyksellä saattaa olla vaikutusta ajotapaan, niin jokaisella kuljettajalle käytetään erilaista järjestystä (mahdolliset järjestykset ovat ABC, ACB, BAC, BCA, CAB, CBA).

Polttoaineen kulutukset olivat oheisen taulukon mukaiset.

SPSS ja toistomittausten varianssianalyysi

Kuten muissakin keskiarvoon perustuvissa menetelmissä, niin myös toistomittausten varianssianalyysissä tarkasteltavien muuttujien edellytetään olevan normaalijakautuneita. Isoilla otoksilla (yli 30) asiaa ei yleensä tarvitse murehtia, mutta pienillä otoksilla normaalijakautuneisuus on syytä testata. Testaamiseen voin käyttää Explore-toimintoa. Lue lisää artikkelistani SPSS: Explore. Esimerkkitapauksessamme Explore-toiminnon tuottamien normaalijakaumatestien p-arvot ovat suurempia kuin 0,05, joten normaalijakautuneisuus voidaan olettaa.

Toistomittausten varianssianalyysiä ei ole SPSS:n peruspaketissa. Toiminto on käytettävissä, jos käytössäsi on Advanced Statistics -lisäpaketti.

• Valitse Analyze > General Linear Model > Repeated Measures…
• Kirjoita Within-Subject Factor Name -ruutuun ryhmittelevän tekijän nimi (Säätö) ja Number of Levels -ruutuun ryhmien lukumäärä (3).
• Napsauta Add-painiketta.
• Kirjoita Measure name -ruutuun mitattavan ominaisuuden nimi (Kulutus).
• Napsauta Add-painiketta.
• Napsauta Define-painiketta, jolloin pääset Repeated Measures -ikkunaan.

• Siirrä vasemman reunan muuttujat (A, B, C) yksi kerrallan Within-Subjects Variables -ruutuun.

Plots-painikkeen takaa kannattaa valita tulostettavaksi kuvio, josta nähdään havainollisesti eri säätöjen keskiarvot. Napsauta Plots, siirrä ryhmittelevä tekijä (Säätö) Horizontal Axis -ruutuun, napsauta Add ja napsauta Continue.

Options-painikkeen takaa kannattaa tehdä muutama asetus: 

• Siirrä ryhmittelevä tekijä (Säätö) Display Means for -ruutuun.
• Valitse Compare main effects.
• Valitse Confidence interval adjustment -alasvetovalikosta haluamasi menetelmä parivertailujen laskemiseen. Parivertailujen tekemisessä on sama problematiikka kuin yksisuuntaisessa varianssianalyysissä. Jos et halua perehtyä asiaan syvällisemmin, niin voit valita alasvetovalikosta Bonferroni-korjauksen.
• Valitse Descriptive statistics tunnuslukutaulukon tulostamiseksi.
• Napsauta lopuksi Options-ikkunan Continue-painiketta.

Tulostaulukoiden lukeminen

Tuloksena saat häkellyttävän paljon taulukoita, joista kaikkia et luultavasti tarvitse. Seuraavassa käsitellään vain perustapauksessa tarvittavia taulukoita. Descriptive Statistics -taulukosta näet eri säätöihin liittyvien kulutusten keskiarvot ja keskihajonnat.

Toistomittausten varianssianalyysiin kuuluu olennaisena osana sfäärisyyden (sphericity) testaaminen. Yksinkertaistaen voisi todeta, että tässä testataan ryhmien välisten erojen varianssien yhtäsuuruutta. Lisätietoa saat englanninkielisen Wikipedian artikkelista Mauchly’s sphericity test.

Jos Mauchlyn sfäärisyystestin p-arvo (Sig,) on yli 0,05, niin Tests of Within-Subjects Effects -taulukosta luetaan Sphericity Assumed -riviä. Muussa tapauksessa käytetään esimerkiksi Greenhouse-Geisser -korjattua testiä.

Jos Tests of Within-Subjects Effects -taulukon p-arvo (Sig.) on alle 0,05, niin voidaan päätellä, että vähintään yhden parin välillä on merkitsevä ero? Seuraavaksi pitää selvittää minkä parien välillä on merkitsevää eroa. Tämä selviää Pairwise Comparisons -taulukosta. Seuraavaan taulukkoon on laskettu parivertailut Bonferroni-korjausta käyttäen.

Säätöjen B (taulukossa 2) ja C (taulukossa 3) kohdalla on merkitsevä ero (p–arvo 0,007). Kulutusten erojen keskiarvon luottamusväli on 0,168 – 0,698 litraa. Muiden parien välillä ei ole merkitsevää eroa.

Webropol raportit

En päivitä enää tätä Webropol 2.0 artikkelia. Suosittelen käyttämään uudempaa Webropol 3.0 versiota.

Päivitetty 25.4.2013

Tämä artikkeli ei korvaa Webropolin raportointiopasta, mutta voi auttaa sinut nopeasti alkuun. Lue raportointiopasta, jos tämän artikkelin ohjeet eivät riitä. Kirjauduttuasi Webropoliin löydät raportointioppaan seuraavasti:

• Napsauta MyWebropol (oikealla ylhäällä).
• Valitse keskimmäisestä (Suomi) alasvetovalikosta Webropol 2.0 Raportointiopas.

Raportin luominen

Pääset katsomaan vastausten yhteenvedon valitsemalla Raportti ja yhteenveto -välilehdellä ylhäältä vasemmalta Perusraportti. Perusraportti avautuu erilliseen ikkunaan (sinun täytyy ehkä sallia ponnahdusikkunat). Jos vastausten yhteenveto ei tule suoraan näkyviin, niin valitse alasvetovalikosta katsottavaksi raportiksi Perusraportti. Perusraportti näyttää valintakysymykset pylväskaavioina ja asteikkokysymykset taulukoina, joissa on lukumäärät ja keskiarvot.

Voit suodattaa eli poimia tarkasteltavaksi tiettyyn kysymykseen tietyllä tavalla vastanneet (Suodata) tai voit ristiintaulukoida vastauksia valitsemasi kysymyksen vastausten kanssa (Vertaile vastaajaryhmiä).

Voit säätää taulukoiden ja kaavioiden asetuksia (Kuvaajien asetukset ja Kuvaajien ulkoasu). Voit valita, mitkä kysymykset näytät raportissa (Valitse mitkä kysymykset näytetään raportissa).

Muokatun perusraportin voit tallentaa nimellä (Tallenna nimellä). Tallennettuihin raportteihin pääset myöhemmin vasemman yläkulman alasvetovalikon kautta.

Muokatussa raportissa pääset yksittäisen kysymyksen asetuksiin Asetukset-painikkeella:

Asetusten Vastausvaihtoehtojen asetukset -välilehdellä voit määrittää arvot, joita ei huomioida keskiarvojen laskennassa. Poista tarkoittaa, että arvoa ei oteta mukaan keskiarvon ja muiden tunnuslukujen laskentaan. Seuraavassa vastausvaihtoehtoa 6 (Ei kokemusta asiasta) ei oteta mukaan keskiarvoihin. Arvo kuitenkin näkyy lukumäärä- ja prosenttitaulukoissa, koska vaihtoehtoa Piilota ei ole valittu.

Webropol numeroi asteikon vaihtoehdot siten että ensimmäinen vaihtoehto on 1, toinen vaihtoehto 2 jne. Tarvittaessa voit vaihtaa numeroinnin muuttamalla Painoarvo-sarakkeen lukuja. Tällä on vaikutusta keskiarvoihin.

Lopuksi voit sulkea asetukset napsauttamalla Käytä ja sulje -painiketta.

Raportti Exceliin

Voit viedä raportin Exceliin jatkotyöstettäväksi:

• Valitse oikealta ylhäältä Vie-alasvetovalikosta Excel.
• Valitse Kysymysyhteenvedot per välilehti.
• Napsauta Vie-painiketta.
• Avaa tai tallenna Excel-tiedosto.

Voit muokata taulukoita ja kaavioita Excelin tavanomaisilla toiminnoilla.

Raportin julkaiseminen

Raportin yläreunan Lisätoiminnot-valikosta voit julkaista raportin (Julkaise raportti). Webropol antaa julkaistun raportille linkin (nettiosoitteen). Jos et lukitse nykyisiä vastauksia, niin nettiosoitteessa oleva raportti päivittyy automaattisesti uusien vastausten myötä.

Analysoi

Raportin kunkin kysymyksen vieressä oikealla on Analysoi-linkki. Linkki vie Insight-ohjelmaan, jossa voit valita muiden muassa

• Yleiskuva (perustunnusluvut ja korrelaatiokertoimet)
• Tarkastele (korrelaatiokertoimet ja niiden p-arvot)

Kunkin Insight-taulukon oikeassa yläreunassa on Excel-kuvake, jolla voit viedä taulukon Exceliin.

Muita Webropol-artikkeleita

• Webropol: kyselyn laatiminen
• Webropol: kyselyn julkaiseminen
• Webropolilla kerätty aineisto analysoitavaksi
• Webropol: Text Mining

Analyyseihin sopivat tietokoneohjelmat

Päivitetty 8.11.2019.

Analyysien onnistumiseksi on tärkeää tietää mitä haluat laskea? Jollet tiedä, niin katsele tiekarttoja.

Excel

Excelillä voit laskea lukumäärä- ja prosenttiyhteenvedot, ristiintaulukoinnit sekä tilastolliset tunnusluvut. Lasketuista taulukoista saat helposti havainnollisia graafisia esityksiä. Excelissä on monipuoliset mahdollisuudet tulostaulukoiden ja graafisten esitysten muotoiluun. Tilastollisen merkitsevyyden testaamiseen Excel ei ole paras mahdollinen väline eikä kaikkiin tapauksiin löydy valmista toimintoa.

Jos osaat Excelin perustaidot, niin Excel on luonteva valinta perusanalyyseihin. Tilastollisen merkitsevyyden testaukseen voit käyttää esimerkiksi Pythonia tai SPSS:ää. Excel-muotoon tallennettu data aukeaa Pythonilla tai SPSS:llä.

Python

Jos et karsasta koodaamista, niin kannattaa opetella analysoimaan Python-ohjelmointikielellä. Aikaisempaa ohjelmointi/koodaus-kokemusta et tarvitse. Python  ohjelmakirjastoineen on joustava, tehokas ja ilmainen väline datojen analysointiin, p-arvojen laskentaan ja visualisointiin.

Python sopii erinomaisesti myös koneoppimisen malleihin ja ennakoivaan analytiikkaan.

Lue lisää:

• Miksi Python?
• Data-analytiikka Pythonilla.

Tilasto-ohjelmat

Tilasto-ohjelmat ovat varta vasten tilastoaineistojen analysointiin tarkoitettuja ohjelmia ja näin ollen varma valinta datan analysointiin. Tilastollisen merkitsevyyden testaus (khiin neliö -testi, t-testit, korrelaation merkitsevyys, Mann-Whitney -testi jne.) sujuu tilasto-ohjelmalla helposti. Tilasto-ohjelmista käytetyimpiä on SPSS.

Pienen opettelun jälkeen SPSS on helppokäyttöinen ohjelma, jolla voit analysoida myös alunperin Excel-muotoon tallennettuja datoja. Graafisten esitysten laatiminen vaatii hieman enemmän opettelua.

Lisätietoa SPSS-tilastohjelmasta.

Nettikyselyohjelmistot

Webropol, SurveyMonkey, Questback ja muut vastaavat ovat nettikyselyn tekemiseen sopivia ohjelmistoja. Niiden avulla saat myös joitain analyysejä nettikyselyn vastauksista. Monipuolisuudeltaan ja joustavuudeltaan ne eivät ole Excelin, Pythonin tai SPSS:n veroisia. Voit hyödyntää niiden tuottamia taulukoita ja graafisia esityksiä harkintasi mukaan. Useimmissa tapauksissa nettikyselyn raakadata täytyy kuitenkin tuoda Exceliin, Pythoniin tai tilasto-ohjelmaan monipuolisempien analyysien tekemiseksi.

Lisätietoa Webropolista.

Pääsääntö

Pääsääntö: Käytetty tietokoneohjelma ei ole itsetarkoitus. Olennaista on, että käytät tilanteeseen sopivia menetelmiä, olet huolellinen sekä esität tulokset selkeästi ja havainnollisesti.

Tiekartat

Päivitetty 24.1.2020

Datoja jalostetaan ja analysoidaan, jotta saadaan käyttökelpoista, havainnollista ja ymmärrettävää tietoa päätöksenteon tueksi ja perusteluksi.

Analysoitavia datoja saadaan erilaisista lähteistä, esimerkiksi

• mittalaitteilla mitattuja ilmansaasteiden pitoisuuksia
• kyselylomakkeella kerättyjä mielipiteitä
• kokeellisella tutkimusasetelmalla kerättyjä havaintoja
• verkkosivuston käyttötilastoja
• yrityksen tietokannasta poimittuja myyntitapahtumia
• internetin tietokannoista löytyviä tilastoja.

Datoja jalostetaan ja analysoidaan, jotta saadaan käyttökelpoista, havainnollista ja ymmärrettävää tietoa päätöksenteon tueksi ja perusteluksi. Analysointiin käytetään samoja menetelmiä datan lähteestä riippumatta.

Analyysit aloitetaan muuttujakohtaisilla tarkasteluilla muuttuja kerrallaan (kuvaileva analytiikka). Joissain tapauksissa  muuttujakohtaiset tarkastelut riittävät, mutta yleensä analyyseissä edetään riippuvuuksien tarkasteluun (selittävä analytiikka). Yksinkertaisimmillaan  tarkastellaan kahden muuttujan välistä riippuvuutta. Jos toinen muuttujista on kategorinen, niin riippuvuuden sijasta voidaan puhua ryhmien vertailusta: kategorisen muuttujan arvot määräävät ryhmät, joiden välillä toisen muuttujan arvoja vertaillaan. Jos molemmat muuttujat ovat määrällisiä niin riippuvuutta voidaan kutsua korrelaatioksi ja sen voimakkuutta mitataan korrelaatiokertoimen avulla.

Edellä todetun perusteella voin jaotella perusanalyysit seuraavasti:

Vaativammassa analyysissä käytetään monimuuttujamenetelmiä, joissa analysoidaan useamman muuttujan välisiä riippuvuuksia samanaikaisesti.

Seuraavassa luettelen kuhunkin analyysityyppiin liittyviä menetelmiä. Ryhmittelen menetelmät sen mukaan minkälaisille mitta-asteikoille ne sopivat. Käyttämäni mitta-asteikot ovat

• Kategorinen: Muuttujan arvot luokittelevat havaintoyksiköt toisensa poissulkeviin kategorioihin/luokkiin. Tällaista mitta-asteikkoa kutsutaan myös luokitteluasteikoksi, nominaaliasteikoksi ja laatueroasteikoksi. Esimerkki: Henkilön ammatti.
• Järjestysasteikollinen: Jos kategoriat/luokat voidaan asettaa yksikäsitteiseen suuruus, paremmuus tai muuhun järjestykseen, niin kyseessä on järjestysasteikko. Tällaista mitta-asteikkoa kutsutaan myös ordinaaliasteikoksi. Esimerkki: Hotelliluokituksessa hotellin saama tähtien määrä.
• Määrällinen: Muuttujan arvot mittaavat mitattavan ominaisuuden määrää numeroasteikolla. Määrälliset muuttujat kattavat sekä välimatka-asteikolliset (intervalliasteikolliset) että suhdeasteikolliset muuttujat. Esimerkki: Henkilön kuukausipalkka.
• Mielipideasteikko: Mielipideasteikko on järjestysasteikko, mutta monissa tapauksissa sen voidaan ajatella mittaavan mielipiteen, esimerkiksi tyytyväisyyden, määrää numeroasteikolla. Tällöin mielipideasteikko voidaan tulkita määrälliseksi ja määrällisille muuttujille soveltuvia menetelmiä voidaan käyttää. Esimerkki: Tyytyväisyys asiakaspalvelun ystävällisyyteen asteikolla 1-5 (1=erittäin tyytymätön, 5=erittäin tyytyväinen).

Yhden muuttujan tarkastelu

Datan analysoinnin aloitan muuttujakohtaisilla tarkasteluilla.

• Kategorisille muuttujille lasken lukumäärä- ja prosenttitaulukot. Lukumäärä- ja prosenttitaulukosta käytetään myös nimityksiä yhteenvetotaulukko ja frekvenssitaulukko. Taulukoinneissa pääset hyvään alkuun lukemalla artikkelin Taulukointi.
• Järjestysasteikollisille muuttujille voin lukumäärä- ja prosenttitaulukoiden lisäksi laskea viiden luvun yhteenvedon.
• Määrällisille muuttujille lasken tunnuslukuina keskiarvon, keskihajonnan ja viiden luvun yhteenvedon. Tunnusluvuissa pääset hyvään alkuun lukemalla artikkelin Tunnuslukuja.

Mielipideasteikot (esimerkiksi 1-5, täysin eri mieltä – täysin samaa mieltä) ovat järjestysasteikoita, mutta tietyin varauksin voin käyttää keskiarvoa ja keskihajontaa. Voit lukea lisää artikkelista Mielipideasteikon keskiarvo.

Jos analysoitava data on otos laajemmasta perusjoukosta, niin kannattaa laskea prosenttiosuuksille ja keskiarvoille luottamusvälit. Luottamusväli ilmaisee epävarmuuden yleistettäessä prosenttiosuus tai keskiarvo laajempaan perusjoukkoon. Lisätietoa prosenttiosuuden luottamusvälistä artikkelissa Prosenttiosuuden luottamusväli ja keskiarvon luottamusvälistä artikkelissa Keskiarvon virhemarginaali.

Kahden ryhmän vertailu – riippumattomat ryhmät

Päädyn vertailemaan kahta ryhmää esimerkiksi seuraavissa tapauksissa:

• Haluan verrata kyselytutkimusdatan perusteella miesten ja naisten mielipiteitä.
• Haluan verrata kokeellisen tutkimuksen keinoin ovatko alkoholia nauttineiden reaktioaikojen keskiarvot samat kuin alkoholia nauttimattomien.

Jos mitattava muuttuja on kategorinen, niin vertaan lukumääriä ja/tai prosentteja ristiintaulukoimalla ryhmittelevän muuttujan ja mitattavan muuttujan. Hyvään alkuun ristiintaulukoinneissa pääset lukemalla artikkelin Ristiintaulukointi. Jos mitattava muuttuja on määrällinen, niin yleensä vertaan keskiarvoja. Myös mielipideasteikon tapauksessa voin tietyin varauksin verrata keskiarvoja. Lisätietoa artikkelissa Kahden riippumattoman otoksen vertailu.

Tarvittaessa voin testata ryhmien välisen eron merkitsevyyttä. Testaamisella varmistan, onko otoksessa havaittu ero niin suuri, ettei se voi aiheutua pelkästä otantavirheestä, vaan taustalla on ryhmien todellinen ero perusjoukossa. Lisätietoa artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Useamman ryhmän vertailu – riippumattomat ryhmät

Jos vertailtavia ryhmiä on useampia, niin järjestysasteikollisen ja määrällisen muuttujan tapauksessa testimenetelmät ovat erilaiset kuin kahden ryhmän vertailussa.

Lisätietoa testimenetelmistä artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Kahden ryhmän vertailu – riippuvat ryhmät

Kokeellisessa tutkimuksessa päädytään usein vertailemaan toisistaan riippuvia ryhmiä. Jos riippumattoman ja riippuvan ero ei ole sinulle selvä, niin lue artikkeli Riippumattomat vai riippuvat otokset.

Lisätietoa testimenetelmistä artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Useamman ryhmän vertailu – riippuvat ryhmät

Useamman riippuvan ryhmän vertailua tarvitaan lähinnä kokoeellisessa tutkimuksessa.

Lisätietoa testimenetelmistä artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Korrelaatio

Korrelaatio tarkoittaa kahden muuttujan välistä riippuvuutta.

• Kategoristen muuttujien välistä korrelaatiota tarkastelen ristiintaulukoimalla. Tätä jo tarkastelin aiemmin ryhmien vertailun yhteydessä.
• Jos toinen tai molemmat muuttujista ovat järjestysasteikollisia, niin voin laskea Spearmanin järjestyskorrelaation. Joissain tapauksissa Spearmanin järjestyskorrelaatio on sopiva menetelmä myös mielipideasteikollisille muuttujille. Järjestyskorrelaatiosta lisää artikkelissa Spearmanin järjestyskorrelaatio.
• Jos molemmat muuttujat ovat määrällisiä, niin tarkastelen riippuvuutta hajontakaavioiden ja korrelaatiokertoimien avulla. Tästä lisää artikkelissa Korrelaatio ja sen merkitsevyys.

Tarvittaessa voin testata riippuvuuden/korrelaation merkitsevyyttä. Testaamisella varmistan, onko otoksessa havaittu riippuvuus/korrelaatio niin suuri, ettei se voi aiheutua pelkästä otantavirheestä, vaan taustalla on todellinen riippuvuus/korrelaatio perusjoukossa. Lisätietoa testaamisesta artikkelissa Korrelaatio ja sen merkitsevyys.

Mallit ja ennakoiva analytiikka

Edellä mainitut menetelmät sopivat kuvailevaan ja selittävään analytiikkaan. Tarvittaessa voidaan edetä pidemmälle:

• Sovittamalla dataan havaittuja eroja ja riippuvuuksia selittäviä malleja.
• Ennakoimalla tulevaa malleista laskettujen ennusteiden avulla.

Muuttujien mitta-asteikot vaikuttavat mallin valintaan:

• Jos selitettävä muuttuja on määrällinen, niin kyseeseen tulevat erilaiset regressiomallit.
• Jos selitettävä muuttuja on kategorinen, niin kyseeseen tulevat erilaiset luokittelumallit, esimerkiksi logistinen regressio.
• Jos selitettävä muuttuja puuttuu, niin kyseeseen tulevat erilaiset klusterointimallit, esimerkiksi K-means klusterointi.

SPSS: Friedman-testi

Päivitetty 26.9.2020

Useamman kuin kahden riippuvan otoksen välisen eron merkitsevyyttä voin testata toistomittausten varianssianalyysillä. Varianssianalyysin käyttökelpoisuus on kyseenalaista ainakin seuraavissa tapauksissa:

• Otoskoot ovat pieniä (alle 30) eikä ole varma ovatko tarkasteltavat muuttujat normaalijakautuneet perusjoukossa.
• Tarkasteltavat muuttujat ovat mielipideasteikollisia. Jos olen sitä mieltä, että keskiarvo ei ole sopiva tunnusluku mielipideasteikolle, niin varianssianalyysi ei tule kyseeseen.

Varianssianalyysin sijasta voin käyttää Friedman-testiä, jonka kohdalla ei tarvitse olettaa normaalijakautuneisuutta. Friedman-testi soveltuu hyvin mielipideasteikoille.

Excelissä ei ole valmista toimintoa Friedman-testin laskemiseen. Onneksi versiosta 18 lähtien SPSS on sisältänyt erittäin helppokäyttöisen ja havainnollisen tavan testin laskemiseen. Vaikka suorittaisitkin muut analyysit Excelissä, niin tämän testin osalta kannattaa piipahtaa SPSS:n puolella. Tämä on helppoa vaikka et olisi aiemmin SPSS:ää käyttänytkään. Jos SPSS ei ole sinulle entuudestaan tuttu, niin haluat ehkä tutustua monisteeseeni spss.pdf.

Excel-datan avaaminen

Jos data on tallennettu Excel-muotoon artikkelini Datan tallentaminen ohjeiden mukaisesti, niin voit avata sen SPSS-ohjelmaan:

• Valitse SPSS:n käynnistyksen yhteydessä avautuvasta ikkunasta Open an existing data source ja napsauta OK. Jos olit jo ohittanut kyseisen ikkunan, niin valitse valikosta File-Open-Data.
• Valitse avaamisen määrittelyikkunassa tiedostomuodoksi Excel.
• Valitse avattava tiedosto.
• Napsauta Open-painiketta, jolloin avautuu Opening Excel Data Source -valintaikkuna.
• Valitse valintaruutu Read variable names…
• Tarkista ja vaihda tarvittaessa Worksheet ja Range -määrittelyt, jotka määrittelevät mistä taulukosta ja miltä solualueelta aineisto löytyy.
• OK.

Muuttujien mitta-asteikon tarkistaminen

Siirry Variable View -näkymään napsauttamalla vastaavaa välilehteä SPSS-ikkunan alareunassa. Tarkista tarkasteltavien muuttujien mitta-asteikko Measure-sarakkeesta. Jos mitta-asteikko on Nominal tai Ordinal, niin vaihda asteikoksi Scale.

Miksi tarkasteltavien muuttujien mitta-asteikon täytyy olla Scale? Testin taustaoletuksena on, että muuttuja on perimmiltään jatkuvaluonteinen. Esimerkiksi 5-portaisen tyytyväisyys-asteikon arvot eivät sellaisenaan ole jatkuvaluonteisia. Tässä kuitenkin riittää se, että oletetaan tyytyväisyys jatkuvaluonteiseksi muuttujaksi, vaikka sitä mitataankin tarkkuudella 1, 2, 3, 4, 5.

Testin suorittaminen

Seuraavassa on käytetty SPSS-muotoista kahvi.sav -dataa (tallenna data tietokoneellesi ja avaa se sen jälkeen SPSS-ohjelmaan).

Datassa on yhdeksän arvioijan arviot (eri arviointikohteiden yhteispistemäärä) neljästä kahvimerkistä (A, B, C ja D). Kahvimerkkien eroja voisi testata toistomittausten varianssianalyysillä, mutta normaalijakautuneisuuden testaus osoittaa normaalijakautuneisuuden kyseenalaiseksi kahvimerkin B kohdalla (Shapiro-Wilk -testin p-arvo 0,017). Voit lukea lisää normaalijakautuneisuuden testaamisesta artikkelistani SPSS: Explore.

Friedman-testin laskeminen sujuu seuraavasti:

• Valitse valikosta Analyze – Nonparametric Tests – Related Samples. Avautuvan Nonparametric Tests: Two or More Related Samples -ikkunan yläreunassa on kolme välilehteä: Objective, Fields ja Settings.
• Valitse Objective-välilehdeltä Automatically compare observed data to hypothesized.
• Valitse Fields-välilehdeltä vaihtoehto Use custom field assignments ja siirrä tarkasteltavat muuttujat Test Fields: -ruutuun.
• Napsauta Run-painiketta.

Testin tulkinta

Testin tulosteena saat havainnollisen tulostaulukon.

Taulukosta löytyy testattu nollahypoteesi, testimenetelmän nimi (Friedman’s…), p-arvo ja testin johtopäätös. Johtopäätöksen kriteerinä SPSS käyttää oletusarvoisesti merkitsevyystasoa 0,05 (nollahypoteesi hylätään, jos p-arvo on alle 0,05). Merkitsevyystason voit halutessasi vaihtaa Settings-välilehden Test Options -kohdasta.

Testin mukaan ainakin joidenkin kahvimerkkien välillä on eroa (p-arvo < 0,01). SPSS tarjoaa lisätietoa ja graafisia havainnollistuksia Model Viewer -ikkunassa jos kaksoisnapsautat tulostaulukkoa. Jos valitset Model Viewer -ikkunan View-alasvetovalikosta (kahdesta View-alasvetovalikosta oikeanpuoleinen) Pairwise Comparisons, niin saat parivertailut:

Parivertailujen korjatut p-arvot (Adj. Sig.) on laskettu jakamalla parivertailun p-arvo vertailtavien parien kokonaismäärällä (6). Korjattujen p-arvojen mukaan merkitseviä eroja on kahvimerkkien D ja A, D ja B sekä C ja B välillä.

Toistomittausten varianssianalyysi

Päivitetty 25.4.2019.

Jos tarkoituksena on tutkia aiheuttavatko käsittelyt eroja tutkittavien ominaisuuksiin, niin keskeisimmät tutkimusasetelmat ovat:

Satunnaistettu koe (completely randomized design): Jokaista käsittelyä varten arvotaan oma ryhmä tutkittavia. Tällöin analyysimenetelmänä käytetään yksisuuntaista varianssianalyysiä.

Toistomittaus (repeated measures design): Käytetään samaa tutkittavien joukkoa eri käsittelyillä. Tätä kutsutaan toistomittaukseksi, koska samoja tutkittavia mitataan toistuvasti eri käsittelyillä. Tällöin analyysimenetelmäksi sopii toistomittausten varianssianalyysi. Esimerkiksi kolmen erilaisen moottorin säädön vaikutusta polttoaineen kulutukseen voidaan tutkia kuuden eri kuljettajan avulla siten, että kukin kuljettaja ajaa testilenkin jokaisella säädöllä. Mittaus toistetaan siis kullekin kuljettajalle 3 kertaa, mutta jokaisella kerralla on erilainen säätö.

Satunnaistettu lohkokoe (randomized block design): Jos tiedetään, että jokin tutkittavien ominaisuus vaikuttaa mittauksen kohteena oleviin muuttujiin, niin tutkittavat voidaan jakaa kyseisen ominaisuuden mukaan samanlaisiin lohkoihin. Esimerkiksi samaan pikaruokaketjuun kuuluvien neljän ravintolan eroja voidaan arvioida jakamalla arvioijat kokemuksen mukaan kuuteen eri lohkoon seuraavasti:

• ensimmäiseen lohkoon otetaan vain kaikkein kokeneimmat arvioijat
• toiseen lohkoon otetaan hieman vähemmän kokeneet arvioijat jne.
• kuudenteen lohkoon otetaan kaikkein vähiten kokemusta omaavat arvioijat
• kuhunkin lohkoon otetaan neljä arvioijaa, koska arvoitavia ravintoloita on neljä
• samaan lohkoon kuuluville neljälle arvioijalle arvotaan satunnaisesti arvioitavat ravintolat.

Asetelmalla pyritään kontrolloimaan arvioijan kokemuksen vaikutusta arvioihin. Myös tähän asetelmaan sopii analyysimenetelmäksi toistomittausten varianssianalyysi.

Yksisuuntaisen varianssinalyysin ja toistomittausten varianssianalyysin keskeinen ero

Yksisuuntaisessa varianssianalyysissä mittaustulosten vaihtelu jaetaan ryhmien (kutakin käsittelyä vastaa yksi ryhmä) väliseen ja ryhmien sisäiseen vaihteluun. Kyseessä on malli, jossa pyritään selittämään vaihtelu ryhmien (käsittelyjen) eroilla ja tässä mallissa kaikki muu kuin ryhmien välinen vaihtelu on luettavissa virhevaihteluksi.

Toistomittausten varianssianalyysissä erotetaan ryhmien sisäisestä vaihtelusta lohkojen välinen vaihtelu ja muu osa ryhmien sisäisestä vaihtelusta luetaan virhevaihteluksi. Kyseessä on malli, jossa pyritään selittämään vaihtelu ryhmien eroilla ja lohkojen eroilla. Muu kuin ryhmien välinen ja lohkojen välinen vaihtelu luetaan virhevaihteluksi. Virhevaihtelu jää pienemmäksi kuin yksisuuntaisessa varianssianalyysissä, koska lohkojen välinen vaihtelu otetaan malliin mukaan.

Ryhmien välisten erojen merkitsevyyttä mitataan ryhmien välisen vaihtelun ja virhevaihtelun suhteena. Jos ryhmien vaihtelu on riittävän paljon virhevaihtelua suurempi, niin sillon ryhmien välisiä eroja voidaan pitää merkitsevinä. On siis olennaista, että käytetään mallia, jossa virhevaihtelu saadaan mahdollisimman pieneksi. Näin ollen toistomittausasetelmassa ja satunnaistetussa lohkoasetelmassa kannatta aina käyttää toistomittausten varianssianalyysiä yksinkertaisen varianssianalyysin sijasta.

Toistomittausten varianssianalyysi Excelillä

Esimerkki. Auton polttoaineen kulutusta verrattin kolmella erilaisella moottorin säädöllä A, B ja C. Testikuljettajina oli 6 kuljettajaa, jotka ajoivat arvotussa järjestyksessä testilenkin kullakin säädöllä. Mitatut kulutukset (litraa sadalla kilomertrilla) olivat oheisen taulukon mukaiset.

Excelin analyysityökalujen avulla voin laskea toistomittausten varianssianalyysin. Jos et ole aiemmin ottanut analyysityökaluja käyttöön, niin voit tehdä sen seuraavasti:

• Valitsen File – Options (Tiedosto – Asetukset).
• Valitsen Add Ins (Apuohjelmat) ja valitsen alhaalta Manage (Hallinta) -ruudusta Excel Add Ins (Excel-apuohjelmat).
• Valitsen Go (Siirry).
• Valitsen luettelosta Analysis Toolpak (Analyysityökalut) ja valitsen OK.
• Tämän jälkeen löydän Data (Tiedot) -välilehdeltä analyysityökalut (Data Analysis).

Analyysityökaluista löydän toistomittausten varianssianalyysin nimellä Anova: Two-Factor Without Replication (Anova: kaksisuuntainen ilman toistoa). Nimitys kaivannee hieman selitystä: ’kaksisuuntainen’ viittaa siihen, että yhteisvaihtelua selitetään kahdella tekijällä, käsittelyllä ja tutkittavien/lohkojen eroilla; ’ilman toistoa’ viittaa siihen, että kullakin käsittelyn ja tutkittavan/lohkon yhdistelmällä on vain yksi mittaus.

Täytän Anova-ikkunaan syöttöalueen (Input Range). Syöttöalueeksi valitsen kaikki kulutukset sekä rivi- ja sarakeotsikot. Lisäksi määritän, että otsikot huomioidaan (Labels).

Excel tulostaa keskiarvot ja varianssit sekä ANOVA-taulukon, joka näyttää seuraavalta:

ANOVA-taulukossa vaihtelu on jaettu kolmeen osaan:

• rivien eli tässä tapauksessa kuljettajien väliseen vaihteluun (SS=0,55205)
• sarakkeiden eli tässä tapauksessa säätöjen väliseen vaihteluun (SS=0,573333)
• muuhun vaihteluun eli virhevaihteluun (SS=0,196067).

Mitä suurempi säätöjen välinen vaihtelu on virhevaihteluun verrattuna, sitä merkitsevämpiä eroja säätöjen välillä on. Tämä testataan F-testillä, jonka p-arvon voin lukea taulukosta.

Esimerkin tapauksessa ainakin kahden säädön välillä on merkitsevä ero (p-arvo 0,001).

On opettavaista ainakin kerran tutustua ANOVA-taulukon johtamiseen ja erityisesti vaihtelua mittaavien neliösummien (SS, sum of squares) laskemiseen. Voit tutustua ANOVA-taulukon johtamiseen Excel-tiedoston anovakaavat.xlsx avulla. Olen laskenut tiedostoon Excelin kaavoilla kaikki ANOVA-taulukossa oleva luvut. Tiedostosta löytyy laskettu esimerkki myös satunnaistetusta lohkokokeesta.

Käyttöedellytykset

Toistomittausten varianssianalyysiä koskee sama käyttöedellytys kuin muitakin keskiarvon käyttöön perustuvia menetelmiä: otoskeskiarvojen täytyy olla peräisin likimain normaalijakaumasta. Jos ryhmät ovat isoja (vähintään 30), niin normaalijakautuneisuus ei yleensä ole ongelma. Jos ryhmät ovat pieniä, voin arvioida normaalijakautuneisuutta otoksen arvojen jakauman perusteella (histogrammi, ruutu- ja janakaavio). Epäselvissä tapauksissa kannattaa testata normaalijakautuneisuus SPSS:llä. Ohjeet laatikkokaavion tekemiseen ja normaalijakautuneisuuden testaamiseen löydät artikkelistani SPSS: Explore.

Toisena käyttöedellytyksenä on niin kutsuttu sfäärisyys (sphericity). Yksinkertaistaen voisi todeta, että tässä on kyse ryhmien välisten erojen varianssien yhtäsuuruudesta. Sfäärisyyden testaamiseen ei ole toimintoa Excelissä. Lue lisää artikkelista SPSS: Toistomittausten varianssianalyysi.

Jos käyttöedellytykset eivät täyty, niin voin käyttää SPSS:n Friedman-testiä.

Parivertailut

Varianssianalyysi kertoo onko ryhmien keskiarvojen välillä merkitseviä eroja. Sen sijaan varianssianalyysi ei kerro minkä ryhmien välillä on merkitseviä eroja. Arvailuja voin tehdä ryhmien keskiarvojen perusteella. Tarkempaan analyysiin tarvitsen parivertailuja. Excel ei tarjoa valmiita työkaluja parivertailujen tekemiseen. SPSS sisältää menetelmiä parivertailujen tekemiseen. Lue lisää artikkelista SPSS: Toistomittausten varianssianalyysi.

Prosenttiosuuden luottamusväli

Päivitetty 25.4.2019.

Otoksesta laskettu prosenttiosuus kertoo prosenttiosuuden otoksessa. Jos yleistän otoksesta lasketun prosenttiosuuden laajempaan perusjoukkoon, niin minun täytyy huomoida otantavirheen aiheuttama epävarmuus. Otantavirheen aiheuttaman epävarmuuden ilmaisen virhemarginaalin avulla. Voin arvioida 95 % virhemarginaalin seuraavasti:

Kaavassa n tarkoittaa otoskokoa ja p otoksesta laskettua prosenttiosuutta desimaalimuodossa. Jos np>10 ja n(1−p)>10, niin voin pitää kaavan antamaa arviota hyvänä. Jos esimerkiksi otoskoko on 100, niin kaava antaa hyviä arvioita virhemarginaalille prosenttiosuuden ollessa 10 % ja 90 % välillä. Monissa lähteissä ehdosta esitetään lievempi versio np>5 ja n(1-p)>5.

Voit käyttää virhemarginaalin laskentaan Exceliin laatimaani laskuria virhemarginaali.xlsx. Laskuri laskee prosenttiosuuden virhmarginaalin, jos annat otoksesta lasketun prosenttiosuuden ja otoskoon.

Esimerkki. Uuden ydinvoimalan kannattajien osuus oli 800 henkilön kyselytutkimuksessa 40,8 %. Virhemarginaaliksi lasken

Usein virhemarginaalin pohjalta muodostetaan luottamusväli. Luottamusvälin alarajan saan vähentämällä otosprosenttiosuudesta virhemarginaalin ja ylärajan saan lisäämällä otosprosenttiosuuteen virhmarginaalin

Esimerkki. Edellisen esimerkin tapauksessa 95 % luottamusväli on 0,374 – 0,442. Tärmä tarkoittaa sitä että 95 % varmuudella todellinen prosenttiosuus sisältyy luottamusväliin 37,4 % – 44,2 %.

Mihin virhemarginaalin laskenta perustuu

Esimerkiksi uuden ydinvoimalan kannattajien lukumäärä otoksessa noudattaa binomijakaumaa. Binomijakauma seuraa siitä, että jokainen otokseen otettu joko kannattaa uutta ydinvoimalaa tai ei. Binomijakaumahan on nimen omaan jakauma tällaisille kaksiarvoisille tilanteille. Binomijakaumaa voidaan isoilla otoksilla approksimoida normaalijakauman avulla (edellä mainitut ehdot np>10 ja n(p-1)>10 takaavat, että approksimaatio on riittävän hyvä käytännön sovelluksiin). Voidaankin siis todeta, että isoilla otoksilla otoksesta laskettu prosenttiosuus on peräisin likimain normaalijakaumasta. Kyseisen normaalijakauman keskihajonta eli prosenttiosuuden keskivirhe on

Normaalijakauman ominaisuuksista seuraa, että otoksesta laskettu prosenttiosuus on 95 % varmuudella korkeintaan 1,96 keskivirheen päässä jakauman keskiarvosta eli perusjoukon todellisesta prosenttiosuudesta.

Kääntäen, 95 % varmuudella perusjoukon todellinen prosenttiosuus on korkeintaan 1,96 keskivirheen päässä otosprosenttiosuudesta. Tällä perusteella prosenttiosuuden 95 % virhemarginaali on 1,96 keskivirhettä.

Normaalijakaumaan liittyvä arvo 1,96 on likiarvo. Tarkemman arvon voit laskea Excelin funktiolla

=NORM.S.INV(97,5%) (suom. NORM_JAKAUMA.KÄÄNT)

Funktion argumenttina voi käyttää myös 2,5%, mutta tällöin vastaus tulee negatiivisella etumerkillä varustettuna.

Tärkeää

Virhemarginaalin arvo on luotettava ainoastaan jos otos on valittu perusjoukosta asianmukaista otantamenetelmää käyttäen.

Muita menetelmiä virhemarginaalin arviointiin

Kuten aiemmin totesin, niin pienillä otoksilla tai pienillä/suurilla prosenttiosuuksilla edellä esitettyä approksimaatiota ei voi pitää hyvänä. On kehitetty useita vaihtoehtoisia ja parempia (ja mutkikkaampia) menetelmiä prosenttiosuuden virhemarginaalin arviointiin. Lisätietoa englanninkielisen Wikipedian artikkelista Binomial proportion confidence interval ja artikkelista The Annals of Statistics 2002, Vol. 30, No. 1, 160–201: Confidence intervals for a binomial proportion and asymptotic expansions.

SPSS ja prosenttiosuuden luottamusväli

SPSS ei sisällä yksinkertaista toimintoa prosenttiosuuden luottamusvälin laskentaan. Tämä on luonnollisesti aiheuttanut monien mielissä ihmetystä. Lue IBM:n vastaus asiasta esitettyyn kysymykseen: http://www-01.ibm.com/support/docview.wss?uid=swg21474963.