Päivitetty 20.4.2019.
Jos haluan tutkia vaikuttaako alkoholi miesten reaktioaikaan, niin voin toimia seuraavasti:
- valitsen kaksi toisistaan riippumatonta otosta miehiä
- ensimmäisen otoksen miehille mittaan reaktioajan ilman alkoholin vaikutusta
- toisen otoksen miehille mittaan reaktioajan sen jälkeen kun he ovat nauttineet tarkoin mitatun määrän alkoholia
- lasken kummallekin otokselle reaktioaikojen keskiarvon.
Mitä enemmän otosten keskiarvot poikkeavat toisistaan sitä enemmän minulla on perusteita väittää, että alkoholi vaikuttaa miesten reaktioaikaan. Pienet erot keskiarvoissa voivat selittyä otantavirheellä. Reaktioajoissa on luontaista vaihtelua miesten välillä ja on sattuman varassa minkälaisen reaktioajan omaavat miehet otoksiin valikoituvat. Otantavirheen osuus on sitä pienempi mitä suurempaa otosta käytän.
Kysymys: Miten voin tietää selittyykö keskiarvojen ero pelkästään otantavirheellä vai onko taustalla myös alkoholin vaikutus reaktioaikaan?
Vastaus: Suoritan kahden riippumattoman otoksen t-testin. T-testin tuloksena saan p-arvon. P-arvo on todennäköisyys sille, että keskiarvojen ero selittyy pelkästään otantavirheellä. Mitä pienempi p-arvo sitä enemmän saan tukea sille, että keskiarvojen välinen ero on merkitsevä.
Vakiintuneen tavan mukaan alle 0,050 (5,0 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa olevan eron puolesta.
Testin suorittamiseksi minun täytyy valita suoritanko yhtäsuurten vai erisuurten varianssien testin sekä suoritanko kaksisuuntaisen vai yksisuuntaisen testin. Lisäksi minun on syytä pohtia, onko testin suorittaminen ylipäätään luotettavaa eli täyttyvätkö testin käyttöedellytykset.
Mitä pienempi p-arvo sitä enemmän saan tukea sille, että keskiarvojen välinen ero on merkitsevä.
Yhtäsuurten vai erisuurten varianssien testi?
Kahden riippumattoman otoksen t-testistä on kaksi versiota.
- Yhtäsuurten varianssien testi sopii tilanteisiin, joissa verrattavien ryhmien varianssit (varianssi on keskihajonnan toinen potenssi) ovat likimain yhtäsuuret.
- Erisuurten varianssien testiä taas voidaan käyttää tilanteisiin, joissa verrattavien ryhmien varianssien yhtäsuuruutta ei voida olettaa.
Kysymys: Mistä tiedän pitääkö käyttää yhtäsuurten vai erisuurten varianssien testiä?
Vastaus: Jos olet epävarma, niin käytä erisuurten varianssien testiä. Jos tiedät perusjoukoissa varianssien olevan likimain yhtäsuuret ja otosten varianssitkin tukevat tätä käsitystä, niin voit käyttää yhtäsuurten varianssien testiä.
Jos olet epävarma, niin käytä erisuurten varianssien testiä.
Kaksisuuntainen vai yksisuuntainen testi?
Jos etukäteen ajateltuna kumman tahansa ryhmän keskiarvo voi olla toista suurempi, niin käytän kaksisuuntaista testiä.
Jos etukäteen ajateltuna vain toisen ryhmän keskiarvo voi olla suurempi tai olen yksinomaan kiinnostunut toisen ryhmän keskiarvon suuremmuudesta, niin voin käyttää yksisuuntaista testiä. Yksisuuntaisessa testauksessa keskiarvojen tilastollisesti merkitsevä ero saavutetaan pienemmällä keskiarvojen erolla.
Testin käyttöedellytykset
Ensiksi tarkasteltavan muuttujan täytyy olla sellainen, että keskiarvon laskeminen on mielekästä.
Jos otoskoot ovat vähintään 30, niin voin käyttää testiä. Tätä pienempien otosten tapauksessa edellytetään, että tarkasteltava muuttuja on perusjoukossaan likimain normaalisti jakautunut. Jotkin muuttujat ovat luonnostaan sellaisia, että normaalijakautuneisuus voidaan olettaa. Reaktioaika on tällainen muuttuja (useimmat ihmisen fyysisistä ja psyykkisistä ominaisuuksista noudattavat normaalijakaumaa). Epäselvissä tapauksissa voin yrittää arvioida normaalijakautuneisuutta otoksen arvojen jakauman perusteella (voin käyttää esimerkiksi histogrammia tai ruutu- ja janakaaviota).
Testin p-arvon laskeminen Excelillä
Voin laskea testin p-arvon Excelin funktiolla =T.TEST(otos1;otos2;suuntaisuus;tyyppi)
- otos1: viittaus ensimmäiseen otokseen
- otos2: viittaus toiseen otokseen
- suuntaisuus: 2 kaksisuuntaiselle testille, 1 yksisuuntaiselle testille
- tyyppi: 2 yhtäsuurten varianssien testille, 3 erisuurten varianssien testille
Suomenkielisessä Excelissä funktion nimi on T.TESTI.
Funktion nimeä vaihdettiin Excelin versioon 2010. Aikasemmissa versioissa funktion nimi on TTEST (TTESTI). Vanha funktion nimi toimii edelleen uudemmissa Excelin versioissa.
Esimerkki. Tiedostossa reaktioajat.xlsx on kuvitteellinen esimerkkiaineisto reaktioajoista. Ensimmäisen otoksen reaktioajat ovat soluissa C2:C16 ja toisen otoksen reaktioajat soluissa C17:C31. P-arvon laskemiseen (kaksisuuntainen, erisuurten varianssien testi) voin käyttää funktiota =T.TEST(C2:C16;C17:C31;2;3)
Esimerkkiaineiston p-arvo on noin 0,006 (0,6 %), mikä tarkoittaa tilastollisesti merkitsevää keskiarvojen eroa.
Testin tulosten raportointi
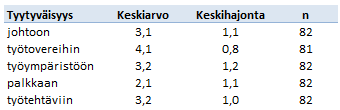
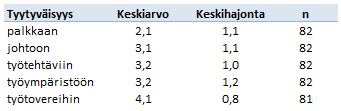
Tuloksen voin raportoida monellakin tavalla. Tärkeintä on, että otosten keskiarvot, keskihajonnat, otoskoot ja testin p-arvo ovat näkyvillä. Esimerkiksi:
Alkoholia nauttineiden reaktioaikojen keskiarvo 0,237 sekuntia (keskihajonta = 0,035, n=15) poikkesi raittiiden reaktioaikojen keskiarvosta 0,205 sekuntia (keskihajonta = 0,020, n=15). Ero osoittautui riippumattomien otosten t-testillä merkitseväksi: t(22) = -3,045, p = 0,006, 2-suuntainen.
Tieteellisessä tekstissä t-testimuuttujan arvo täytyy ilmoittaa yhdessä vapausasteluvun df kanssa: t(22) = -3,045. Testimuuttujan arvon ja vapausasteluvun saat Excelin analyysityökaluilla (katso reaktioajat.xlsx) tai käyttämällä valmista laskentapohjaa tiedostossa otantavirhe.xlsx.
SPSS
Jos haluat suorittaa testauksen SPSS:llä, niin lue artikkelini SPSS: Kahden riippumattoman otoksen vertailu.
Muita menetelmiä kahden riippumattoman otoksen vertailuun
Kahden riippumattoman otoksen t-testi soveltuu kokeelliseen tutkimusasetelmaan, jossa vertaillaan kahta riippumatonta otosta, kuten tämän artikkelin reaktioaika-esimerkissä. Testiä voidaan käyttää myös ei-kokeellisissa tutkimusasetelmissa. Esimerkiksi kyselytutkimusainestossa voidaan verrata eläkeläisten ja työssäkäyvien TV:n katseluun käytettyä aikaa.
Jos kahden riippumattoman otoksen t-testi ei tule kysymykseen, niin tarjolla on monia muita menetelmiä ryhmien välisen eron testaamiseen. Lue lisää artikkelistani Onko ryhmien välinen ero tilastollisesti merkitsevä?
Kahden riippuvan otoksen vertailu
Miesten reaktioaikaa voin tutkia myös toisenlaisella tutkimusasetelmalla:
- valitsen otoksen miehiä
- mittaan otoksen miehille reaktioajan ilman alkoholin vaikutusta
- mittaan otoksen miehille reaktioajan sen jälkeen kun he ovat nauttineet tarkoin mitatun määrän alkoholia
- lasken kullekin miehelle reaktioaikojen eron
- lasken reaktioaikojen erojen keskiarvon.
Kumpaakin mittausta voin pitää omana otoksenaan, mutta kyseessä ovat toisistaan riippuvat otokset (kyseessähän ovat samat miehet). Tällaisessa asetelmassa otosten vertailuun täytyy käyttää riippuvien otosten t-testiä.
Usein kysyttyä
Kysymys: Olen laskenut keskiarvot ja keskihajonnat, mutta alkuperäinen aineisto ei ole Excelissä. Voinko silti laskea kahden otoksen t-testin.
Vastaus: Voit. Käytä Exceliin laatimaani laskentapohjaa otantavirhe.xlsx. Syötä laskentapohjaan molempien otosten otoskoot, keskiarvot ja keskihajonnat.
Kysymys: Millä tavoin erisuurten ja yhtäsuurten varianssien t-testien laskentatavat eroavat toisistaan?
Vastaus: Lue lisätietoa.
Kysymys: Voinko laskea virhemarginaalin otoskeskiarvojen erolle?
Vastaus: Kyllä. Lue lisätietoa ja käytä Exceliin laatimaani laskentapohjaa otantavirhe.xlsx. Syötä laskentapohjaan molempien otosten otoskoot, keskiarvot ja keskihajonnat.