Korrelaatio – lisätietoa

Päivitetty 19.4.2019.

Kovarianssi

Kahden muuttujan, x ja y, välisen suoraviivaisen riippuvuuden voimakkuutta voidaan mitata laskemalla kovarianssi:

Osoittajassa lasketaan x:n ja y:n arvojen poikkeamia keskiarvostaan, kerrotaan poikkeamat keskenään ja lasketaan tulot yhteen. Lopuksi jaetaan vapausastemäärällä (otoskoko-1), jolloin saadaan keskimääräinen poikkeamien tulo eli kovarianssi. Yksi vapausaste on menetetty keskiarvon laskennassa. Huomaathan, että muuttujan kovarianssi itsensä kanssa on sama kuin varianssi. Seuraavassa yritän perustella, miksi kovarianssi sopii suoraviivaisen riippuvuuden mittaamiseen?

Jos hajontakaavioon piirretään pystyviiva kuvaamaan x-arvojen keskiarvoa ja vaakaviiva kuvaamaan y-arvojen keskiarvoa, niin viivat rajaavat neljä neljännestä:

• I neljänneksessä x:n ja y:n poikkeamat keskiarvostaan ovat positiivisia ja näin ollen poikkeamien tulo on positiivinen.
• III neljänneksessä x:n ja y:n poikkeamat keskiarvostaan ovat negatiivisia ja näin ollen poikkeamien tulo on positiivinen.
• II neljänneksessä x:n poikkeamat keskiarvostaan ovat negatiivisia ja y:n poikkeamat keskiarvostaan positiivisia. Näin ollen poikkeamien tulo on negatiivinen.
• IV neljänneksessä x:n poikkeamat keskiarvostaan ovat positiivisia ja y:n poikkeamat keskiarvostaan negatiivisia. Näin ollen poikkeamien tulo on negatiivinen.

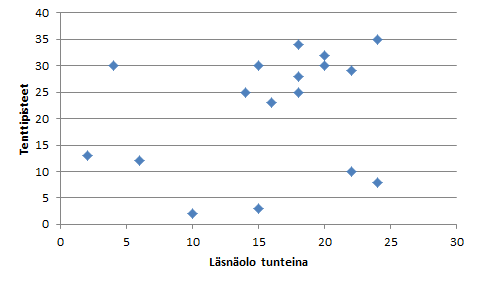
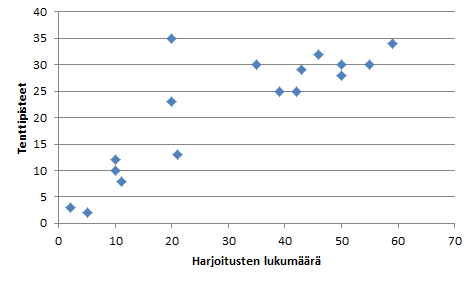
Jos havainnot keskittyvät I ja III neljännekseen, niin kovarianssi on positiivinen (vasemmanpuoleinen kuva). Jos havainnot keskittyvät II ja IV neljännekseen, niin kovarianssi on negatiivinen. Jos havainnot jakautuvat tasaisesti kaikkiin neljänneksiin, niin kovarianssi on likimain nolla.

Pearsonin korrelaatiokerroin

Eri tyyppisten muuttujien välisiä kovariansseja ei voi vertailla keskenään, koska muuttujien mittayksiköt vaikuttavat kovarianssin arvoon. Vertailun mahdollistamiseksi lasketaan kovarianssia hyväksi käyttäen Pearsonin korrelaatiokerroin, joka on muuttujien mittayksiköistä riippumaton tunnusluku. Puhuttaessa korrelaatiokertoimesta tarkoitetaan yleensä juuri Pearsonin korrelaatiokerrointa. Pearsonin korrelaatiokerroin lasketaan jakamalla kovarianssi keskihajontojen tulolla.

Muuttujien järjestys (kumman valitset x-muuttujaksi, kumman y-muuttujaksi) ei vaikuta korrelaatiokertoimen arvoon. Keskihajontojen tulolla jakaminen normittaa korrelaatiokertoimen sellaiseksi, että se voi saada ainoastaan arvoja -1:n ja +1:n väliltä.

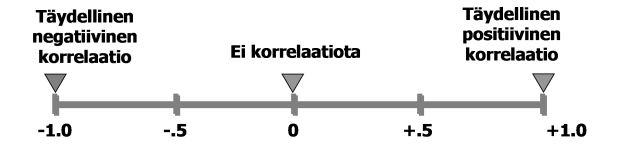
• Korrelaatiokertoimen arvo +1 saavutetaan silloin, kun kaikki hajontakaavion pisteet sijaitsevat samalla nousevalla suoralla.
• Korrelaatiokertoimen arvo -1 saavutetaan silloin, kun kaikki pisteet sijaitsevat samalla laskevalla suoralla.
• Korrelaatiokertoimen arvo 0 merkitsee, ettei muuttujien välillä ole lainkaan suoraviivaista riippuvuutta. Tällöin muuttujien välillä voi toki olla muunlaista kuin suoraviivaista riippuvuutta.

Mitä kauempana korrelaatiokerroin on nollasta, sitä voimakkaammasta suoraviivaisesta riippuvuudesta on kyse.

Korrelaatiokertoimen merkitsevyyden testaaminen

Korrelaation merkitsevyyden testaamiseen liittyvän p-arvon laskenta perustuu seuraavaan testimuuttujaan:

Voidaan osoittaa, että korrelaation ollessa nolla kyseinen testimuuttuja noudattaa Studentin t-jakaumaa vapausastein n-2. Lisätietoa Studentin t-jakaumasta englanninkielisessä Wikipediassa Student’s t-distribution. P-arvo on  todennäköisyys saada kyseisestä t-jakaumasta testimuuttujan suuruinen tai vielä kauempana nollasta oleva arvo. Mitä pienempi p-arvo, sitä enemmän saadaan tukea sille, että korrelaatio on nollasta poikkeava.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Voit käyttää laatimaani laskentapohjaa testaa_korrelaatio.xlsx p-arvon ja luottamusvälin laskentaan. Lähtötietoina tarvitaan korrelaatiokerroin ja otoskoko.

Korrelaatiokertoimen luottamusväli

Korrelaatiokertoimen luottamusvälin laskeminen on hankalahko tehtävä. Excel-pohja testaa_korrelaatio.xlsx laskee luottamusvälin alarajan ja ylärajan, kun lähtötietoina on korrelaatiokerroin ja otoskoko. Laskentapohjassa käytän kaavaa, jonka johtamisen löydät Ilkka Mellinin (2006) monisteesta Tilastolliset menetelmät: Regressioanalyysi sivulta 256.

Korrelaatio ja sen merkitsevyys

Päivitetty 17.4.2019. Tämä on Akin menetelmäblogin luetuin artikkeli!

Hallitset jo toivottavasti ristiintaulukoinnin. Ristiintaulukointi on sopiva menetelmä kahden kategorisen muuttujan riippuvuuden tarkasteluun. Kahden määrällisen muuttujan riippuvuutta puolestaan tarkastellaan hajontakaavion ja korrelaatiokertoimen avulla.

Hajontakaavio

Käytän esimerkkinä tiedostosta korrelaatio.xlsx löytyvää dataa, jossa on kolme muuttujaa: opiskelijan läsnäolo lähiopetustunneilla, suoritettujen harjoitustehtävien lukumäärä ja tentin pistemäärä. Haluan selvittää onko lähiopetustunneille osallistumisella ja suoritettujen harjoitustehtävien lukumäärällä yhteyttä tenttipistemäärään.

Saan havainnollisen kuvan asiasta tekemällä hajontakaaviot. Excelissä hajontakaavio on nimeltään Scatter (Piste). Läsnäolon ja tenttipisteiden välisessä hajontakaaviossa en näe merkittävää yhteyttä, vaan havaintopisteet ovat melko satunnaisesti jakautuneet.

Suoritetut harjoitustehtävät sen sijaan näyttävät olevan positiivisessa yhteydessä tenttipistemäärään. Hajontakaaviossa tämä näkyy selvästi nousevana pisteparvena. Alhaiset harjoitustehtävien määrät näyttävät liittyvän alhaisiin tenttipistemääriin ja korkeat harjoitustehtävien määrät näyttävät liittyvän korkeisiin tenttipistemääriin.

Korrelaatiokerroin

Korrelaatiokerroin on tunnusluku suoraviivaisen riippuvuuden voimakkuudelle. Excelissä voin laskea korrelaation funktiolla CORREL (KORRELAATIO). Funktion ensimmäiseksi lähtötiedoksi annetaan viittaus ensimmäisen muuttujan arvoihin ja toiseksi lähtötiedoksi viittaus toisen muuttujan arvoihin.

Korrelaatiokertoimen arvo voi olla mitä tahansa -1 ja +1 väliltä. Lähellä nollaa olevat kertoimet liittyvät tilanteisiin, joissa ei ole suoraviivaista riippuvuutta. Lähellä +1 olevat kertoimet viittaavaat positiiviseen riippuvuuteen (nouseva pisteparvi hajontakaaviossa) ja lähellä -1 olevat kertoimet viittaavat negatiiviseen riippuvuuteen (laskeva pisteparvi hajontakaaviossa).

Esimerkkidatassa läsnäolon ja tenttipistemäärän välinen korrelaatiokerroin on 0,27 ja harjoitusten ja tenttipistemäärän välinen korrelaatiokerroin on 0,84. Korrelaatiokertoimet siis kertovat samaa kuin hajontakaaviot.

Korrelaation merkitsevyys

Jos data pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Korrelaation tapauksessa tämä tarkoittaa muuttujien välisen korrelaation yleistämistä perusjoukkoon.

Pienet korrelaatiot voin selittää otantavirheellä. Otoksessa havaitun korrelaation täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Suuruutta testaan vertaamalla korrelaatiokerrointa hypoteettiseen tilanteeseen, jossa ei ole lainkaan korrelaatiota (korrelaatiokerroin on 0). Jos otoksesta laskettu korrelaatiokerroin poikkeaa riittävästi nollasta, niin voin kutsua korrelaatiota tilastollisesti merkitseväksi.

Korrelaatiokertoimen merkitsevyyden testaamiseksi lasketaan niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: kuinka todennäköistä on saada havaitun suuruinen tai vielä kauempana nollasta oleva korrelaatiokertoimen arvo ilman että korrelaatiota on perusjoukossa? Mitä pienempi p-arvo on sitä enemmän korrelaation yleistäminen perusjoukkoon saa tukea.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Jos haluat tietää p-arvon laskentaperusteesta, niin lue artikkeli Korrelaatio – lisätietoa.

Voit käyttää p-arvon laskemiseen valmista laskentapohjaa testaa_korrelaatio.xlsx. Kirjoita laskentapohjaan otoskoko ja korrelaatiokerroin, jonka jälkeen voit lukea p-arvon. Käytä 2-suuntaista p-arvoa, jos testaat sitä onko korrelaatio nollasta poikkeava. Käytä 1-suuntaista p-arvoa, jos testaat pelkästään korrelaation positiivisuutta tai pelkästään korrelaation negatiivisuutta.

Jos testaan läsnäolotuntien ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,143 (otoskoko 17, korrelaatiokerroin 0,2746). Tuloksen voin raportoida esimerkiksi seuraavasti (yleisesti käytössä oleva merkintä korrelaatiokertoimelle on r):

Läsnäolotuntien ja tenttipistemäärän välillä ei ole tilastollisesti merkitsevää positiivista korrelaatiota (r=0,27; n=17; 1-suuntaisen testin p-arvo=0,143).

Jos testaan suoritettujen harjoitusten ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,000 (otoskoko 17, korrelaatiokerroin 0,8438). Tuloksen voin raportoida esimerkiksi seuraavasti:

Suoritettujen harjoitusten ja tenttipistemäärän välillä on positiivinen korrelaatio (r=0,84; n=17; 1-suuntaisen testin p-arvo<0,001).

Tilastollisen merkitsevyyden ohella kannattaa pohtia myös käytännön merkitsevyyttä. Korrelaatiokerroin voi olla tilastollisesti merkitsevä ja silti vailla käytännön merkitsevyyttä. Yksinkertainen tapa käytännön merkitsevyyden arviointiin on hajontakaavion tarkastelu. Jos et näe hajontakaavion pisteparvessa merkittävää säännönmukaisuutta niin saattaa olla että korrelaatiolla ei ole käytännön merkitsevyyttä.

Poikkeavat arvot

Hajontakaaviossa selvästi muista poikkeavat pisteet ovat ongelmallisia korrelaatiokerrointa käytettäessä. Lue lisää artikkelista Poikkeavat arvot.

Lisätietoa

Artikkelissa Korrelaatiokerroin – lisätietoa on yksityiskohtaisempaa tietoa korrelaatiokertoimen laskennasta, p-arvon laskennasta ja ohje korrelaatiokertoimen luottamusvälin laskentaan.

SPSS

SPSS tulostaa korrelaatiokerrointen yhteyteen automaattisesti p-arvot. Lue lisää SPSS monisteesta spss19.pdf.