Graafinen esittäminen

Päivitetty 1.2.2019

• Excel-kaavioiden perusteet kaavio.xlsx
• Aikasarjojen esittäminen aikasarjat.xlsx
• Harvinaisempia kaavioita kaavio2.xlsx

Monissa tapauksissa voin havainnollistaa numerotaulukon sisältöä graafisesti. Pidän kuitenkin mielessä kohderyhmän. Numeroihin tottuneelle ja tarkkaa tietoa kaipaavalle kohderyhmälle esitän mieluummin numeroita sisältävän taulukon. Nopeaa yhteenvetoa kaipaavalle ja/tai numeroihin tottumattomalle kohderyhmälle havainnollistan numerotaulukon graafisesti.

Pidän kaaviota laatiessa mielessäni, että laadin kaavion jollekin toiselle, en itselleni. Yritän asettua kaavion katsojan asemaan ja huomioin seuraavat seikat:

• Kaaviolla tulee olla tarkoitus ja tehtävä: minkä tiedon/viestin haluan välittää katsojalle?
• Kaaviolla tulee olla kohderyhmä: kenelle kaavio on tarkoitettu?
• Kokeilen eri vaihtoehtoja ja valitsen tarkoitukseen ja kohderyhmälle parhaiten sopivan esitystavan.
• Kaavion tulee olla selkeä ja helposti ymmärrettävä.
• Johdatan katsojan huomion esitettävään tietoon/viestiin, en kaavion tehosteisiin.
• Esitän tiedot peittelemättä ja rehellisesti.
• Otsikoin akselit ja esitän käytetyt yksiköt selkeästi.
• Ilmoitan tiedon lähteen, jos tieto on peräisin ulkopuolisesta lähteestä.
• Lisään tarvittaessa kaavioon huomautuksia korostaakseni epätavallisten tai poikkeavien arvojen syitä.
• Yhdistän kaavion luontevasti sitä edeltävään tai seuraavaan sanalliseen selitykseen, jossa kerron mihin seikkoihin katsojan kannattaa kaaviossa kiinnittää huomioita. Huomion arvoisia seikkoja ovat yleensä erot, riippuvuudet, poikkeukset tai kehityssuunnat.

Arvosarjat

Kaaviossa esitän yhden tai useampia arvosarjoja (data series). Arvosarjat voivat ilmetä kaaviossa esimerkiksi seuraavilla tavoilla:

• Jos esitän yhden arvosarjan pylväskaaviona, niin kaaviossa on vain yhden värisiä pylväitä. Yksi pylväs vastaa aina yhtä arvosarjan arvoa.
• Jos esitän pylväskaaviossa useamman arvosarjan, niin jokaista arvosarjaa vastaavat oman värisensä pylväät.
• Jos esitän viivakaaviossa yhden arvosarjan, niin kaaviossa on yksi viiva.
• Jos esitän viivakaaviossa useamman arvosarjan, niin kaaviossa on yksi viiva jokaiselle arvosarjalle.
• Piirakkakaaviossa piirakan siivut vastaavat arvosarjan arvoja.
• Hajontakaaviossa on kaksi yhtä monta arvoa sisältävää arvosarjaa. Ensimmäisen sarjan arvoakselina on vaaka-akseli ja toisen sarjan arvoakselina pystyakseli. Arvosarjojen arvot muodostavat pareja. Jokaista paria vastaa hajontakaavion piste.

Onnistuneen kaavion laatimiseksi arvosarjan arvojen täytyy olla Excel-taulukossa allekkain tai vierekkäin. Taulukkoon kannattaa lisätä otsikot:

• Koko arvosarjan otsikko (nimi) välittömästi arvosarjan yläpuolelle (jos arvosarjan arvot allekkain) tai vasemmalle puolelle (jos arvosarjan arvot vierekkäin).
• Jos arvosarjan yksittäisillä arvoilla on otsikot, niin ne kannattaa sijoittaa taulukkoon arvosarjan vasemmalle puolelle (jos arvosarjan arvot allekkain) tai yläpuolelle (jos arvosarjan arvot vierekkäin).

Yllä näkyvän taulukon kaksi arvosarjaa ovat 17, 15, 6 ja 8, 15, 21. Arvosarjojen nimet ovat Mies ja Nainen. Arvosarjojen yksittäisten arvojen otsikot ovat Tyytymätön, Ei tyytymätön eikä tyytyväinen ja Tyytyväinen. Taulukon arvosarjat voin esittää kaaviona esimerkiksi seuraavasti:

Arvosarjat erottuvat toisistaan eri värisinä ja värit selitetään selitteessä (Legend). Yksittäisten arvojen nimet näkyvät luokka-akselilla (Category axis) ja arvojen suuruus arvoakselilla (Value axis).

Opit kaavioiden laatimiseen liittyvät keskeiset taidot käymällä läpi itseopiskelupaketin kaavio.xlsx ohjein varustetut esimerkit.

Kaaviolajeja

Excelissä on tarjolla monia kaaviolajeja. Suosin useimmille tuttuja kaaviolajeja: vaakapylväskaavio, pystypylväskaavio, viivakaavio ja hajontakaavio.

Vaakapylväskaavio

Excelissä vaakapylväskaaviota kutsutaan palkkikaavioksi (Bar). Vaakapylväskaavio sopii lukumäärien, rahamäärien, prosenttien ja keskiarvojen esittämiseen.

Pystypylväskaavio

Pystypylväskaavio (Column) sopii samankaltaisiin tilanteisiin kuin vaakapylväskaaviokin. Jos pylväät esittävät määrällisen muuttujan luokkia, esimerkiksi palkkaluokkia, niin pylväät laitetaan kiinni toisiinsa.

Viivakaavio

Viivakaavio (Line) on havainnollisin tapa esittää ajallista kehitystä. Esimerkiksi kuukausimyynnit 12 kuukauden ajalta tai bensiinin hinta päivittäin viimeisen kuukauden ajalta kannattaa esittää viivakaaviona. Yksityiskohtaista tietoa ja hyviä niksejä aikasarjojen esittämiseen löydät itseopiskelupaketista aikasarjat.xlsx.

Hajontakaavio

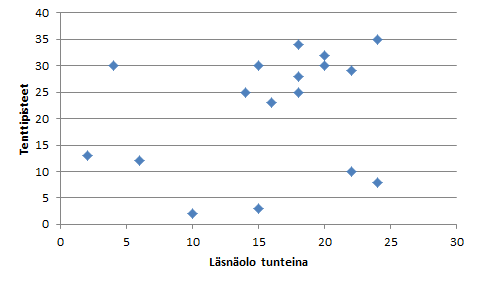
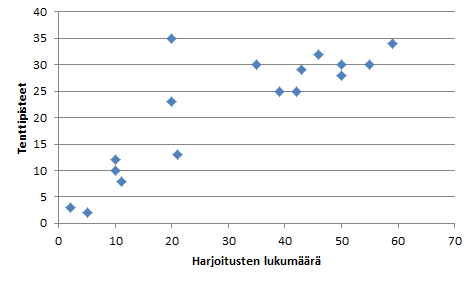
Excelissä hajontakaaviota kutsutaan pistekaavioksi (Scatter). Hajontakaaviosta käytetään myös nimitystä sirontakaavio. Hajontakaavion taustalla on kaksi samanmittaista arvosarjaa, joiden arvot muodostavat pareja. Hajontakaavion avulla nähdään, onko kahden arvosarjan välillä riippuvuutta. Esimerkiksi seuraavasta hajontakaaviosta näen, onko opiskelijan kurssin aikana tekemien harjoitusten lukumäärän ja tenttipisteidän välillä riippuvuutta?

Piirakkakaavio

Excelissä piirakkakaaviota kutsutaan ympyräkaavioksi (Pie). Piirakkakaaviolla voin havainnollistaa kokonaisuuden jakaantumista osiin. Piirakkakaaviota käytettäessä kaikkien kokonaisuuden osien täytyy olla mukana: Jos esimerkiksi esitän älypuhelintyyppien (Android, iPhone, Windows Phone) markkinaosuuksia piirakkana, niin mukana täytyy olla myös siivu edustamassa muita puhelintyyppejä.

Piirakkakaavion käyttöä kohtaan voidaan esittää kritiikkiä. Lue lisää artikkelista Paha piirakkakaavio.

Harvinaisempia kaavioita

Haluaisitko laatia Excelillä pyramidikaavion, mielipideprofiilin, Ganttin kaavion tai funktion kuvaajan. Onnistuu: kaavio2.xlsx.

Korrelaatio ja sen merkitsevyys

Päivitetty 17.4.2019. Tämä on Akin menetelmäblogin luetuin artikkeli!

Hallitset jo toivottavasti ristiintaulukoinnin. Ristiintaulukointi on sopiva menetelmä kahden kategorisen muuttujan riippuvuuden tarkasteluun. Kahden määrällisen muuttujan riippuvuutta puolestaan tarkastellaan hajontakaavion ja korrelaatiokertoimen avulla.

Hajontakaavio

Käytän esimerkkinä tiedostosta korrelaatio.xlsx löytyvää dataa, jossa on kolme muuttujaa: opiskelijan läsnäolo lähiopetustunneilla, suoritettujen harjoitustehtävien lukumäärä ja tentin pistemäärä. Haluan selvittää onko lähiopetustunneille osallistumisella ja suoritettujen harjoitustehtävien lukumäärällä yhteyttä tenttipistemäärään.

Saan havainnollisen kuvan asiasta tekemällä hajontakaaviot. Excelissä hajontakaavio on nimeltään Scatter (Piste). Läsnäolon ja tenttipisteiden välisessä hajontakaaviossa en näe merkittävää yhteyttä, vaan havaintopisteet ovat melko satunnaisesti jakautuneet.

Suoritetut harjoitustehtävät sen sijaan näyttävät olevan positiivisessa yhteydessä tenttipistemäärään. Hajontakaaviossa tämä näkyy selvästi nousevana pisteparvena. Alhaiset harjoitustehtävien määrät näyttävät liittyvän alhaisiin tenttipistemääriin ja korkeat harjoitustehtävien määrät näyttävät liittyvän korkeisiin tenttipistemääriin.

Korrelaatiokerroin

Korrelaatiokerroin on tunnusluku suoraviivaisen riippuvuuden voimakkuudelle. Excelissä voin laskea korrelaation funktiolla CORREL (KORRELAATIO). Funktion ensimmäiseksi lähtötiedoksi annetaan viittaus ensimmäisen muuttujan arvoihin ja toiseksi lähtötiedoksi viittaus toisen muuttujan arvoihin.

Korrelaatiokertoimen arvo voi olla mitä tahansa -1 ja +1 väliltä. Lähellä nollaa olevat kertoimet liittyvät tilanteisiin, joissa ei ole suoraviivaista riippuvuutta. Lähellä +1 olevat kertoimet viittaavaat positiiviseen riippuvuuteen (nouseva pisteparvi hajontakaaviossa) ja lähellä -1 olevat kertoimet viittaavat negatiiviseen riippuvuuteen (laskeva pisteparvi hajontakaaviossa).

Esimerkkidatassa läsnäolon ja tenttipistemäärän välinen korrelaatiokerroin on 0,27 ja harjoitusten ja tenttipistemäärän välinen korrelaatiokerroin on 0,84. Korrelaatiokertoimet siis kertovat samaa kuin hajontakaaviot.

Korrelaation merkitsevyys

Jos data pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Korrelaation tapauksessa tämä tarkoittaa muuttujien välisen korrelaation yleistämistä perusjoukkoon.

Pienet korrelaatiot voin selittää otantavirheellä. Otoksessa havaitun korrelaation täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Suuruutta testaan vertaamalla korrelaatiokerrointa hypoteettiseen tilanteeseen, jossa ei ole lainkaan korrelaatiota (korrelaatiokerroin on 0). Jos otoksesta laskettu korrelaatiokerroin poikkeaa riittävästi nollasta, niin voin kutsua korrelaatiota tilastollisesti merkitseväksi.

Korrelaatiokertoimen merkitsevyyden testaamiseksi lasketaan niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: kuinka todennäköistä on saada havaitun suuruinen tai vielä kauempana nollasta oleva korrelaatiokertoimen arvo ilman että korrelaatiota on perusjoukossa? Mitä pienempi p-arvo on sitä enemmän korrelaation yleistäminen perusjoukkoon saa tukea.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Jos haluat tietää p-arvon laskentaperusteesta, niin lue artikkeli Korrelaatio – lisätietoa.

Voit käyttää p-arvon laskemiseen valmista laskentapohjaa testaa_korrelaatio.xlsx. Kirjoita laskentapohjaan otoskoko ja korrelaatiokerroin, jonka jälkeen voit lukea p-arvon. Käytä 2-suuntaista p-arvoa, jos testaat sitä onko korrelaatio nollasta poikkeava. Käytä 1-suuntaista p-arvoa, jos testaat pelkästään korrelaation positiivisuutta tai pelkästään korrelaation negatiivisuutta.

Jos testaan läsnäolotuntien ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,143 (otoskoko 17, korrelaatiokerroin 0,2746). Tuloksen voin raportoida esimerkiksi seuraavasti (yleisesti käytössä oleva merkintä korrelaatiokertoimelle on r):

Läsnäolotuntien ja tenttipistemäärän välillä ei ole tilastollisesti merkitsevää positiivista korrelaatiota (r=0,27; n=17; 1-suuntaisen testin p-arvo=0,143).

Jos testaan suoritettujen harjoitusten ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,000 (otoskoko 17, korrelaatiokerroin 0,8438). Tuloksen voin raportoida esimerkiksi seuraavasti:

Suoritettujen harjoitusten ja tenttipistemäärän välillä on positiivinen korrelaatio (r=0,84; n=17; 1-suuntaisen testin p-arvo<0,001).

Tilastollisen merkitsevyyden ohella kannattaa pohtia myös käytännön merkitsevyyttä. Korrelaatiokerroin voi olla tilastollisesti merkitsevä ja silti vailla käytännön merkitsevyyttä. Yksinkertainen tapa käytännön merkitsevyyden arviointiin on hajontakaavion tarkastelu. Jos et näe hajontakaavion pisteparvessa merkittävää säännönmukaisuutta niin saattaa olla että korrelaatiolla ei ole käytännön merkitsevyyttä.

Poikkeavat arvot

Hajontakaaviossa selvästi muista poikkeavat pisteet ovat ongelmallisia korrelaatiokerrointa käytettäessä. Lue lisää artikkelista Poikkeavat arvot.

Lisätietoa

Artikkelissa Korrelaatiokerroin – lisätietoa on yksityiskohtaisempaa tietoa korrelaatiokertoimen laskennasta, p-arvon laskennasta ja ohje korrelaatiokertoimen luottamusvälin laskentaan.

SPSS

SPSS tulostaa korrelaatiokerrointen yhteyteen automaattisesti p-arvot. Lue lisää SPSS monisteesta spss19.pdf.