Korrelaatio ja sen merkitsevyys

Päivitetty 17.4.2019. Tämä on Akin menetelmäblogin luetuin artikkeli!

Hallitset jo toivottavasti ristiintaulukoinnin. Ristiintaulukointi on sopiva menetelmä kahden kategorisen muuttujan riippuvuuden tarkasteluun. Kahden määrällisen muuttujan riippuvuutta puolestaan tarkastellaan hajontakaavion ja korrelaatiokertoimen avulla.

Hajontakaavio

Käytän esimerkkinä tiedostosta korrelaatio.xlsx löytyvää dataa, jossa on kolme muuttujaa: opiskelijan läsnäolo lähiopetustunneilla, suoritettujen harjoitustehtävien lukumäärä ja tentin pistemäärä. Haluan selvittää onko lähiopetustunneille osallistumisella ja suoritettujen harjoitustehtävien lukumäärällä yhteyttä tenttipistemäärään.

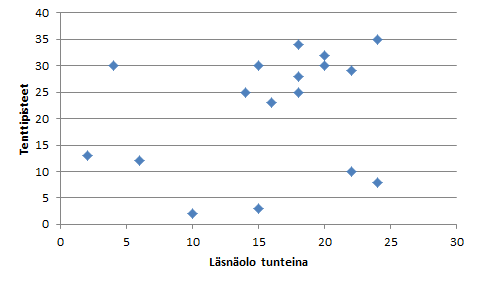
Saan havainnollisen kuvan asiasta tekemällä hajontakaaviot. Excelissä hajontakaavio on nimeltään Scatter (Piste). Läsnäolon ja tenttipisteiden välisessä hajontakaaviossa en näe merkittävää yhteyttä, vaan havaintopisteet ovat melko satunnaisesti jakautuneet.

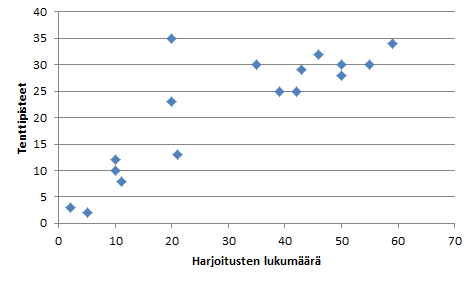
Suoritetut harjoitustehtävät sen sijaan näyttävät olevan positiivisessa yhteydessä tenttipistemäärään. Hajontakaaviossa tämä näkyy selvästi nousevana pisteparvena. Alhaiset harjoitustehtävien määrät näyttävät liittyvän alhaisiin tenttipistemääriin ja korkeat harjoitustehtävien määrät näyttävät liittyvän korkeisiin tenttipistemääriin.

Korrelaatiokerroin

Korrelaatiokerroin on tunnusluku suoraviivaisen riippuvuuden voimakkuudelle. Excelissä voin laskea korrelaation funktiolla CORREL (KORRELAATIO). Funktion ensimmäiseksi lähtötiedoksi annetaan viittaus ensimmäisen muuttujan arvoihin ja toiseksi lähtötiedoksi viittaus toisen muuttujan arvoihin.

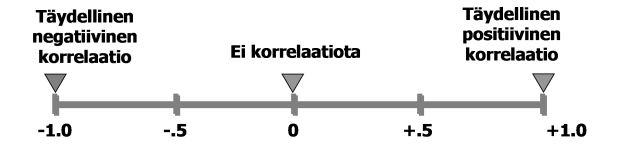
Korrelaatiokertoimen arvo voi olla mitä tahansa -1 ja +1 väliltä. Lähellä nollaa olevat kertoimet liittyvät tilanteisiin, joissa ei ole suoraviivaista riippuvuutta. Lähellä +1 olevat kertoimet viittaavaat positiiviseen riippuvuuteen (nouseva pisteparvi hajontakaaviossa) ja lähellä -1 olevat kertoimet viittaavat negatiiviseen riippuvuuteen (laskeva pisteparvi hajontakaaviossa).

Esimerkkidatassa läsnäolon ja tenttipistemäärän välinen korrelaatiokerroin on 0,27 ja harjoitusten ja tenttipistemäärän välinen korrelaatiokerroin on 0,84. Korrelaatiokertoimet siis kertovat samaa kuin hajontakaaviot.

Korrelaation merkitsevyys

Jos data pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Korrelaation tapauksessa tämä tarkoittaa muuttujien välisen korrelaation yleistämistä perusjoukkoon.

Pienet korrelaatiot voin selittää otantavirheellä. Otoksessa havaitun korrelaation täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Suuruutta testaan vertaamalla korrelaatiokerrointa hypoteettiseen tilanteeseen, jossa ei ole lainkaan korrelaatiota (korrelaatiokerroin on 0). Jos otoksesta laskettu korrelaatiokerroin poikkeaa riittävästi nollasta, niin voin kutsua korrelaatiota tilastollisesti merkitseväksi.

Korrelaatiokertoimen merkitsevyyden testaamiseksi lasketaan niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: kuinka todennäköistä on saada havaitun suuruinen tai vielä kauempana nollasta oleva korrelaatiokertoimen arvo ilman että korrelaatiota on perusjoukossa? Mitä pienempi p-arvo on sitä enemmän korrelaation yleistäminen perusjoukkoon saa tukea.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Jos haluat tietää p-arvon laskentaperusteesta, niin lue artikkeli Korrelaatio – lisätietoa.

Voit käyttää p-arvon laskemiseen valmista laskentapohjaa testaa_korrelaatio.xlsx. Kirjoita laskentapohjaan otoskoko ja korrelaatiokerroin, jonka jälkeen voit lukea p-arvon. Käytä 2-suuntaista p-arvoa, jos testaat sitä onko korrelaatio nollasta poikkeava. Käytä 1-suuntaista p-arvoa, jos testaat pelkästään korrelaation positiivisuutta tai pelkästään korrelaation negatiivisuutta.

Jos testaan läsnäolotuntien ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,143 (otoskoko 17, korrelaatiokerroin 0,2746). Tuloksen voin raportoida esimerkiksi seuraavasti (yleisesti käytössä oleva merkintä korrelaatiokertoimelle on r):

Läsnäolotuntien ja tenttipistemäärän välillä ei ole tilastollisesti merkitsevää positiivista korrelaatiota (r=0,27; n=17; 1-suuntaisen testin p-arvo=0,143).

Jos testaan suoritettujen harjoitusten ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,000 (otoskoko 17, korrelaatiokerroin 0,8438). Tuloksen voin raportoida esimerkiksi seuraavasti:

Suoritettujen harjoitusten ja tenttipistemäärän välillä on positiivinen korrelaatio (r=0,84; n=17; 1-suuntaisen testin p-arvo<0,001).

Tilastollisen merkitsevyyden ohella kannattaa pohtia myös käytännön merkitsevyyttä. Korrelaatiokerroin voi olla tilastollisesti merkitsevä ja silti vailla käytännön merkitsevyyttä. Yksinkertainen tapa käytännön merkitsevyyden arviointiin on hajontakaavion tarkastelu. Jos et näe hajontakaavion pisteparvessa merkittävää säännönmukaisuutta niin saattaa olla että korrelaatiolla ei ole käytännön merkitsevyyttä.

Poikkeavat arvot

Hajontakaaviossa selvästi muista poikkeavat pisteet ovat ongelmallisia korrelaatiokerrointa käytettäessä. Lue lisää artikkelista Poikkeavat arvot.

Lisätietoa

Artikkelissa Korrelaatiokerroin – lisätietoa on yksityiskohtaisempaa tietoa korrelaatiokertoimen laskennasta, p-arvon laskennasta ja ohje korrelaatiokertoimen luottamusvälin laskentaan.

SPSS

SPSS tulostaa korrelaatiokerrointen yhteyteen automaattisesti p-arvot. Lue lisää SPSS monisteesta spss19.pdf.