Tiekartat

Päivitetty 24.1.2020

Datoja jalostetaan ja analysoidaan, jotta saadaan käyttökelpoista, havainnollista ja ymmärrettävää tietoa päätöksenteon tueksi ja perusteluksi.

Analysoitavia datoja saadaan erilaisista lähteistä, esimerkiksi

• mittalaitteilla mitattuja ilmansaasteiden pitoisuuksia
• kyselylomakkeella kerättyjä mielipiteitä
• kokeellisella tutkimusasetelmalla kerättyjä havaintoja
• verkkosivuston käyttötilastoja
• yrityksen tietokannasta poimittuja myyntitapahtumia
• internetin tietokannoista löytyviä tilastoja.

Datoja jalostetaan ja analysoidaan, jotta saadaan käyttökelpoista, havainnollista ja ymmärrettävää tietoa päätöksenteon tueksi ja perusteluksi. Analysointiin käytetään samoja menetelmiä datan lähteestä riippumatta.

Analyysit aloitetaan muuttujakohtaisilla tarkasteluilla muuttuja kerrallaan (kuvaileva analytiikka). Joissain tapauksissa  muuttujakohtaiset tarkastelut riittävät, mutta yleensä analyyseissä edetään riippuvuuksien tarkasteluun (selittävä analytiikka). Yksinkertaisimmillaan  tarkastellaan kahden muuttujan välistä riippuvuutta. Jos toinen muuttujista on kategorinen, niin riippuvuuden sijasta voidaan puhua ryhmien vertailusta: kategorisen muuttujan arvot määräävät ryhmät, joiden välillä toisen muuttujan arvoja vertaillaan. Jos molemmat muuttujat ovat määrällisiä niin riippuvuutta voidaan kutsua korrelaatioksi ja sen voimakkuutta mitataan korrelaatiokertoimen avulla.

Edellä todetun perusteella voin jaotella perusanalyysit seuraavasti:

Vaativammassa analyysissä käytetään monimuuttujamenetelmiä, joissa analysoidaan useamman muuttujan välisiä riippuvuuksia samanaikaisesti.

Seuraavassa luettelen kuhunkin analyysityyppiin liittyviä menetelmiä. Ryhmittelen menetelmät sen mukaan minkälaisille mitta-asteikoille ne sopivat. Käyttämäni mitta-asteikot ovat

• Kategorinen: Muuttujan arvot luokittelevat havaintoyksiköt toisensa poissulkeviin kategorioihin/luokkiin. Tällaista mitta-asteikkoa kutsutaan myös luokitteluasteikoksi, nominaaliasteikoksi ja laatueroasteikoksi. Esimerkki: Henkilön ammatti.
• Järjestysasteikollinen: Jos kategoriat/luokat voidaan asettaa yksikäsitteiseen suuruus, paremmuus tai muuhun järjestykseen, niin kyseessä on järjestysasteikko. Tällaista mitta-asteikkoa kutsutaan myös ordinaaliasteikoksi. Esimerkki: Hotelliluokituksessa hotellin saama tähtien määrä.
• Määrällinen: Muuttujan arvot mittaavat mitattavan ominaisuuden määrää numeroasteikolla. Määrälliset muuttujat kattavat sekä välimatka-asteikolliset (intervalliasteikolliset) että suhdeasteikolliset muuttujat. Esimerkki: Henkilön kuukausipalkka.
• Mielipideasteikko: Mielipideasteikko on järjestysasteikko, mutta monissa tapauksissa sen voidaan ajatella mittaavan mielipiteen, esimerkiksi tyytyväisyyden, määrää numeroasteikolla. Tällöin mielipideasteikko voidaan tulkita määrälliseksi ja määrällisille muuttujille soveltuvia menetelmiä voidaan käyttää. Esimerkki: Tyytyväisyys asiakaspalvelun ystävällisyyteen asteikolla 1-5 (1=erittäin tyytymätön, 5=erittäin tyytyväinen).

Yhden muuttujan tarkastelu

Datan analysoinnin aloitan muuttujakohtaisilla tarkasteluilla.

• Kategorisille muuttujille lasken lukumäärä- ja prosenttitaulukot. Lukumäärä- ja prosenttitaulukosta käytetään myös nimityksiä yhteenvetotaulukko ja frekvenssitaulukko. Taulukoinneissa pääset hyvään alkuun lukemalla artikkelin Taulukointi.
• Järjestysasteikollisille muuttujille voin lukumäärä- ja prosenttitaulukoiden lisäksi laskea viiden luvun yhteenvedon.
• Määrällisille muuttujille lasken tunnuslukuina keskiarvon, keskihajonnan ja viiden luvun yhteenvedon. Tunnusluvuissa pääset hyvään alkuun lukemalla artikkelin Tunnuslukuja.

Mielipideasteikot (esimerkiksi 1-5, täysin eri mieltä – täysin samaa mieltä) ovat järjestysasteikoita, mutta tietyin varauksin voin käyttää keskiarvoa ja keskihajontaa. Voit lukea lisää artikkelista Mielipideasteikon keskiarvo.

Jos analysoitava data on otos laajemmasta perusjoukosta, niin kannattaa laskea prosenttiosuuksille ja keskiarvoille luottamusvälit. Luottamusväli ilmaisee epävarmuuden yleistettäessä prosenttiosuus tai keskiarvo laajempaan perusjoukkoon. Lisätietoa prosenttiosuuden luottamusvälistä artikkelissa Prosenttiosuuden luottamusväli ja keskiarvon luottamusvälistä artikkelissa Keskiarvon virhemarginaali.

Kahden ryhmän vertailu – riippumattomat ryhmät

Päädyn vertailemaan kahta ryhmää esimerkiksi seuraavissa tapauksissa:

• Haluan verrata kyselytutkimusdatan perusteella miesten ja naisten mielipiteitä.
• Haluan verrata kokeellisen tutkimuksen keinoin ovatko alkoholia nauttineiden reaktioaikojen keskiarvot samat kuin alkoholia nauttimattomien.

Jos mitattava muuttuja on kategorinen, niin vertaan lukumääriä ja/tai prosentteja ristiintaulukoimalla ryhmittelevän muuttujan ja mitattavan muuttujan. Hyvään alkuun ristiintaulukoinneissa pääset lukemalla artikkelin Ristiintaulukointi. Jos mitattava muuttuja on määrällinen, niin yleensä vertaan keskiarvoja. Myös mielipideasteikon tapauksessa voin tietyin varauksin verrata keskiarvoja. Lisätietoa artikkelissa Kahden riippumattoman otoksen vertailu.

Tarvittaessa voin testata ryhmien välisen eron merkitsevyyttä. Testaamisella varmistan, onko otoksessa havaittu ero niin suuri, ettei se voi aiheutua pelkästä otantavirheestä, vaan taustalla on ryhmien todellinen ero perusjoukossa. Lisätietoa artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Useamman ryhmän vertailu – riippumattomat ryhmät

Jos vertailtavia ryhmiä on useampia, niin järjestysasteikollisen ja määrällisen muuttujan tapauksessa testimenetelmät ovat erilaiset kuin kahden ryhmän vertailussa.

Lisätietoa testimenetelmistä artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Kahden ryhmän vertailu – riippuvat ryhmät

Kokeellisessa tutkimuksessa päädytään usein vertailemaan toisistaan riippuvia ryhmiä. Jos riippumattoman ja riippuvan ero ei ole sinulle selvä, niin lue artikkeli Riippumattomat vai riippuvat otokset.

Lisätietoa testimenetelmistä artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Useamman ryhmän vertailu – riippuvat ryhmät

Useamman riippuvan ryhmän vertailua tarvitaan lähinnä kokoeellisessa tutkimuksessa.

Lisätietoa testimenetelmistä artikkelissa Onko ryhmien välinen ero tilastollisesti merkitsevä.

Korrelaatio

Korrelaatio tarkoittaa kahden muuttujan välistä riippuvuutta.

• Kategoristen muuttujien välistä korrelaatiota tarkastelen ristiintaulukoimalla. Tätä jo tarkastelin aiemmin ryhmien vertailun yhteydessä.
• Jos toinen tai molemmat muuttujista ovat järjestysasteikollisia, niin voin laskea Spearmanin järjestyskorrelaation. Joissain tapauksissa Spearmanin järjestyskorrelaatio on sopiva menetelmä myös mielipideasteikollisille muuttujille. Järjestyskorrelaatiosta lisää artikkelissa Spearmanin järjestyskorrelaatio.
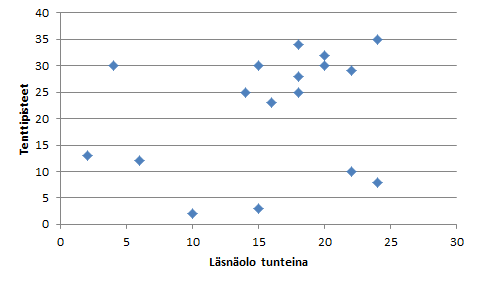
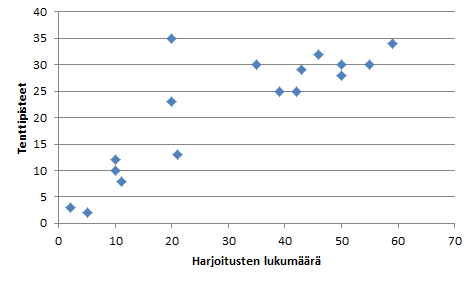
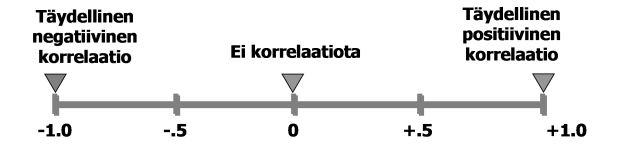
• Jos molemmat muuttujat ovat määrällisiä, niin tarkastelen riippuvuutta hajontakaavioiden ja korrelaatiokertoimien avulla. Tästä lisää artikkelissa Korrelaatio ja sen merkitsevyys.

Tarvittaessa voin testata riippuvuuden/korrelaation merkitsevyyttä. Testaamisella varmistan, onko otoksessa havaittu riippuvuus/korrelaatio niin suuri, ettei se voi aiheutua pelkästä otantavirheestä, vaan taustalla on todellinen riippuvuus/korrelaatio perusjoukossa. Lisätietoa testaamisesta artikkelissa Korrelaatio ja sen merkitsevyys.

Mallit ja ennakoiva analytiikka

Edellä mainitut menetelmät sopivat kuvailevaan ja selittävään analytiikkaan. Tarvittaessa voidaan edetä pidemmälle:

• Sovittamalla dataan havaittuja eroja ja riippuvuuksia selittäviä malleja.
• Ennakoimalla tulevaa malleista laskettujen ennusteiden avulla.

Muuttujien mitta-asteikot vaikuttavat mallin valintaan:

• Jos selitettävä muuttuja on määrällinen, niin kyseeseen tulevat erilaiset regressiomallit.
• Jos selitettävä muuttuja on kategorinen, niin kyseeseen tulevat erilaiset luokittelumallit, esimerkiksi logistinen regressio.
• Jos selitettävä muuttuja puuttuu, niin kyseeseen tulevat erilaiset klusterointimallit, esimerkiksi K-means klusterointi.

Korrelaatio ja sen merkitsevyys

Päivitetty 17.4.2019. Tämä on Akin menetelmäblogin luetuin artikkeli!

Hallitset jo toivottavasti ristiintaulukoinnin. Ristiintaulukointi on sopiva menetelmä kahden kategorisen muuttujan riippuvuuden tarkasteluun. Kahden määrällisen muuttujan riippuvuutta puolestaan tarkastellaan hajontakaavion ja korrelaatiokertoimen avulla.

Hajontakaavio

Käytän esimerkkinä tiedostosta korrelaatio.xlsx löytyvää dataa, jossa on kolme muuttujaa: opiskelijan läsnäolo lähiopetustunneilla, suoritettujen harjoitustehtävien lukumäärä ja tentin pistemäärä. Haluan selvittää onko lähiopetustunneille osallistumisella ja suoritettujen harjoitustehtävien lukumäärällä yhteyttä tenttipistemäärään.

Saan havainnollisen kuvan asiasta tekemällä hajontakaaviot. Excelissä hajontakaavio on nimeltään Scatter (Piste). Läsnäolon ja tenttipisteiden välisessä hajontakaaviossa en näe merkittävää yhteyttä, vaan havaintopisteet ovat melko satunnaisesti jakautuneet.

Suoritetut harjoitustehtävät sen sijaan näyttävät olevan positiivisessa yhteydessä tenttipistemäärään. Hajontakaaviossa tämä näkyy selvästi nousevana pisteparvena. Alhaiset harjoitustehtävien määrät näyttävät liittyvän alhaisiin tenttipistemääriin ja korkeat harjoitustehtävien määrät näyttävät liittyvän korkeisiin tenttipistemääriin.

Korrelaatiokerroin

Korrelaatiokerroin on tunnusluku suoraviivaisen riippuvuuden voimakkuudelle. Excelissä voin laskea korrelaation funktiolla CORREL (KORRELAATIO). Funktion ensimmäiseksi lähtötiedoksi annetaan viittaus ensimmäisen muuttujan arvoihin ja toiseksi lähtötiedoksi viittaus toisen muuttujan arvoihin.

Korrelaatiokertoimen arvo voi olla mitä tahansa -1 ja +1 väliltä. Lähellä nollaa olevat kertoimet liittyvät tilanteisiin, joissa ei ole suoraviivaista riippuvuutta. Lähellä +1 olevat kertoimet viittaavaat positiiviseen riippuvuuteen (nouseva pisteparvi hajontakaaviossa) ja lähellä -1 olevat kertoimet viittaavat negatiiviseen riippuvuuteen (laskeva pisteparvi hajontakaaviossa).

Esimerkkidatassa läsnäolon ja tenttipistemäärän välinen korrelaatiokerroin on 0,27 ja harjoitusten ja tenttipistemäärän välinen korrelaatiokerroin on 0,84. Korrelaatiokertoimet siis kertovat samaa kuin hajontakaaviot.

Korrelaation merkitsevyys

Jos data pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Korrelaation tapauksessa tämä tarkoittaa muuttujien välisen korrelaation yleistämistä perusjoukkoon.

Pienet korrelaatiot voin selittää otantavirheellä. Otoksessa havaitun korrelaation täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Suuruutta testaan vertaamalla korrelaatiokerrointa hypoteettiseen tilanteeseen, jossa ei ole lainkaan korrelaatiota (korrelaatiokerroin on 0). Jos otoksesta laskettu korrelaatiokerroin poikkeaa riittävästi nollasta, niin voin kutsua korrelaatiota tilastollisesti merkitseväksi.

Korrelaatiokertoimen merkitsevyyden testaamiseksi lasketaan niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: kuinka todennäköistä on saada havaitun suuruinen tai vielä kauempana nollasta oleva korrelaatiokertoimen arvo ilman että korrelaatiota on perusjoukossa? Mitä pienempi p-arvo on sitä enemmän korrelaation yleistäminen perusjoukkoon saa tukea.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Jos haluat tietää p-arvon laskentaperusteesta, niin lue artikkeli Korrelaatio – lisätietoa.

Voit käyttää p-arvon laskemiseen valmista laskentapohjaa testaa_korrelaatio.xlsx. Kirjoita laskentapohjaan otoskoko ja korrelaatiokerroin, jonka jälkeen voit lukea p-arvon. Käytä 2-suuntaista p-arvoa, jos testaat sitä onko korrelaatio nollasta poikkeava. Käytä 1-suuntaista p-arvoa, jos testaat pelkästään korrelaation positiivisuutta tai pelkästään korrelaation negatiivisuutta.

Jos testaan läsnäolotuntien ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,143 (otoskoko 17, korrelaatiokerroin 0,2746). Tuloksen voin raportoida esimerkiksi seuraavasti (yleisesti käytössä oleva merkintä korrelaatiokertoimelle on r):

Läsnäolotuntien ja tenttipistemäärän välillä ei ole tilastollisesti merkitsevää positiivista korrelaatiota (r=0,27; n=17; 1-suuntaisen testin p-arvo=0,143).

Jos testaan suoritettujen harjoitusten ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,000 (otoskoko 17, korrelaatiokerroin 0,8438). Tuloksen voin raportoida esimerkiksi seuraavasti:

Suoritettujen harjoitusten ja tenttipistemäärän välillä on positiivinen korrelaatio (r=0,84; n=17; 1-suuntaisen testin p-arvo<0,001).

Tilastollisen merkitsevyyden ohella kannattaa pohtia myös käytännön merkitsevyyttä. Korrelaatiokerroin voi olla tilastollisesti merkitsevä ja silti vailla käytännön merkitsevyyttä. Yksinkertainen tapa käytännön merkitsevyyden arviointiin on hajontakaavion tarkastelu. Jos et näe hajontakaavion pisteparvessa merkittävää säännönmukaisuutta niin saattaa olla että korrelaatiolla ei ole käytännön merkitsevyyttä.

Poikkeavat arvot

Hajontakaaviossa selvästi muista poikkeavat pisteet ovat ongelmallisia korrelaatiokerrointa käytettäessä. Lue lisää artikkelista Poikkeavat arvot.

Lisätietoa

Artikkelissa Korrelaatiokerroin – lisätietoa on yksityiskohtaisempaa tietoa korrelaatiokertoimen laskennasta, p-arvon laskennasta ja ohje korrelaatiokertoimen luottamusvälin laskentaan.

SPSS

SPSS tulostaa korrelaatiokerrointen yhteyteen automaattisesti p-arvot. Lue lisää SPSS monisteesta spss19.pdf.