Merkitsevyyden testaus Pythonilla

Tämän artikkelin ohjelmakoodin ja tulosteet löydät GitHubista:

https://github.com/taanila/tilastoapu/blob/master/p.ipynb

Jos kopioit koodia itsellesi, niin kannattaa käyttää GitHubia. Tästä artikkelista kopioidut koodit eivät välttämättä toimi oikein.

Oletan, että lukijalla on asennettuna Anaconda ja sen mukana tuleva Jupyter notebook.

Otoksessa havaitsemieni erojen ja riippuvuuksien tilastollista merkitsevyyttä voin arvioida laskemalla p-arvon. Pythonin scipy.stats-ohjelmakirjastosta löydän funktiot p-arvojen laskentaan.

Otan ensiksi käyttöön pandas ja scipy.stats -ohjelmakirjastot ja avaan esimerkkinä käyttämäni aineiston:

import pandas as pd
import scipy.stats as stats

df = pd.read_excel('http://taanila.fi/data1.xlsx', 
   sheet_name = 'Data')
df.head()

Korrelaatiokertoimen testaus

Iän ja palkan välisen pearsonin korrelaatiokertoimen ja siihen liittyvän 2-suuntaisen p-arvon saan funktiolla

stats.pearsonr(df['ikä'], df['palkka'])

Jos haluankin käyttää spearmanin järjestyskorrelaatiota, niin saan korrelaatiokertoimen ja 2-suuntaisen p-arvon funktiolla

stats.spearmanr(df['ikä'], df['palkka'])

Korrelaatiokertoimen testaamiseen liittyvistä funktioista löydät lisätietoa scipy.org -sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pearsonr.html#scipy.stats.pearsonr

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.spearmanr.html

Ristiintaulukointi ja khiin neliö -testi

Esimerkiksi sukupuolen ja perhesuhteen väliseen ristiintaulukointiin liittyvän khiin neliö -testin testimuuttujan, p-arvon, vapausasteiden määrän ja odotetut frekvenssit saan funktiolla:

stats.chi2_contingency(pd.crosstab(df['sukup'], 
   df['perhe']))

Lisätietoa khiin neliö -testistä ja sen edeltävyysehdoista löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html#scipy.stats.chi2_contingency

Kahden riippumattoman otoksen t-testi

Jos haluan selvittää, onko miesten ja naisten palkkakeskiarvoissa eroa, niin erotan ensin miesten ja naisten palkat toisistaan (aineistossa 1=mies, 2=nainen)

a=df['palkka'][df['sukup']==1] #Mies
 b=df['palkka'][df['sukup']==2] #Nainen

Tämän jälkeen lasken t-testimuuttujan ja 2-suuntaisen p-arvon funktiolla

stats.ttest_ind(a, b, equal_var=False)

Yllä käytin erisuurten varianssien testiä (equal_var=False).

Lisätietoa riippumattomien otosten t-testistä ja sen edeltävyysehdoista löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html

Mann Whitney U -testi

Jos epäilen t-testin edeltävyysehtojen toteutumista, niin voin testata edellisen esimerkin Mann Whitney U-testillä:

stats.mannwhitneyu(a,b)

Tuloksena saan U-testimuuttujan ja p-arvon. Oletuksena saan 2-suuntaisen p-arvon puolikkaan. Lisätietoa löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.mannwhitneyu.html

Yksisuuntainen varianssianalyysi

Jos haluan selvittää onko eri koulutuksen omaavien keskipalkoissa eroja, niin voin käyttää yksisuuntaista varianssianalyysiä (anova).  Ensiksi erotan eri koulutuksen omaavien palkat toisistaan:

k1=df['palkka'][df['koulutus']==1] #peruskoulu
k2=df['palkka'][df['koulutus']==2] #2. aste
k3=df['palkka'][df['koulutus']==3] #korkeakoulu
k4=df['palkka'][df['koulutus']==4] #ylempi korkeakoulu

Tämän jälkeen lasken anovan F-testimuuttujan ja p-arvon funktiolla:

stats.f_oneway(k1,k2,k3,k4)

Lisätietoa anovasta ja sen edeltävyysehdoista löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.f_oneway.html#scipy.stats.f_oneway

Kruskal-Wallis -testi

Jos epäilet varianssianalyysin edeltävyysehtojen  täyttymistä edellisessä esimerkissä, niin voit käyttää varianssianalyysin sijasta Kruskal-Wallis -testiä:

stats.kruskal(k1, k2, k3, k4)

Tuloksena saat H-testimuuttujan ja p-arvon.

Lisätietoa Kruskal-Wallis-testistä löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kruskal.html#scipy.stats.kruskal

Muita testejä

Lisää merkitsevyystestejä ja muita tilastollisia funktioita löydät scipy.org-sivustolta:

https://docs.scipy.org/doc/scipy/reference/stats.html

 

 

 

 

P-arvo

Päivitetty 25.10.2013.

Tilastollisen testauksen logiikka vastaa monin tavoin oikeudenkäynnin logiikkaa. Oikeudenkäynnissä oletetaan, että henkilö on syytön kunnes toisin osoitetaan. Tilastollisessa testauksessa oletetaan nollahypoteesin pitävän paikkansa kunnes toisin osoitetaan. Nollahypoteesi on usein muotoa ’ei eroa’ tai  ’ei riippuvuutta’. Esimerkiksi

• Miehet ja naiset ovat yhtä tyytyväisiä työympäristöön.
• Tehtyjen harjoitustehtävien määrän ja tenttimenestyksen välillä ei ole riippuvuutta.
• Miesten reaktioaika ei muutu alkoholin nauttimisen seurauksena.

Tilastollisessa testauksessa oletetaan nollahypoteesin pitävän paikkansa kunnes toisin osoitetaan.

Todistustaakka on syyttäjällä, tilastollisessa testauksessa tutkijalla. Syyttäjä kerää oikeudenkäyntiä varten todisteita syyllisyyden puolesta. Tilastollisessa testauksessa tutkija kerää otoksen kiinnostuksen kohteena olevasta perusjoukosta.

Tutkija vertaa otoksen tulosta nollahypoteesiin. Pelkästään otantavirheen takia otoksen tulos poikkeaa enemmän tai vähemmän nollahypoteesista. Isoja poikkeamia ei kuitenkaan voida selittää pelkästään otantavirheellä.  Vastaavalla tavalla syyttäjä voi esittää niin vahvoja todisteita syyllisyyden puolesta, että niitä ei voida selittää pelkästään sattumalla. Jos syytetty on tavattu ryöstön jälkeen ryöstöpaikan läheisyydestä kädessään ryöstösaalista ja toisessa kädessä ase, niin harva uskoo tämän kaiken aiheutuneen sattumalta, ilman että syytetty olisi osallinen ryöstöön.

Pelkästään otantavirheen takia otoksen tulos poikkeaa enemmän tai vähemmän nollahypoteesista. Isoja poikkeamia ei kuitenkaan voida selittää pelkästään otantavirheellä.

Tilastollisen testauksen keskeinen kysymys on: kuinka iso poikkeama nollahypoteesista on liian iso selitettäväksi pelkällä otantavirheellä? Asian selventämiseksi tutkija laskee kuinka yllättävänä otoksessa havaittua voidaan pitää, jos oletetaan nollahypoteesin pitävän paikkansa. Tätä kutsutaan p-arvoksi.

Mitä pienempi p-arvo sitä enemmän vaihtoehtoinen hypoteesi saa tukea ja sitä enemmän todisteet puhuvat nollahypoteesia vastaan.

Jos esimerkiksi tutkija saa p-arvoksi 0,001 eli 0,1 %, niin otoksen tulos on yllättävä. P-arvoa 0,001 on tulkittava seuraavasti: Jos nollahypoteesin oletetaan pitävän paikkansa, niin otoksen kaltainen tai vielä enemmän nollahypoteesista poikkeava tulos sattuu kohdalle yhdessä otoksessa tuhannesta. Kyseessä on siis melko yllättävä tulos. Tämä jos mikä on riittävä todiste nollahypoteesia vastaan. Tuloshan ei nimittäin olekaan enää yllättävä, jos nollahypoteesi ei pidäkään paikkansa. Seuraavassa kolme näkökulmaa p-arvon ymmärtämiseksi:

• P-arvo on todennäköisyys sille, että otoksen tulos poikkeaa havaitun verran tai vieläkin enemmän nollahypoteesista (kun oletetaan, että nollahypoteesi pitää paikkansa).
• P-arvo on todennäköisyys sille, että havaittu poikkeama nollahypoteesista voidaan selittää pelkästään otantavirheellä.
• Jos nollahypoteesi päätetään hylätä, niin p-arvo ilmoittaa päätökseen liittyvän erehtymisriskin.

Mitä pienempi p-arvo sitä enemmän vaihtoehtoinen hypoteesi saa tukea ja sitä enemmän todisteet puhuvat nollahypoteesia vastaan. Kuinka pieni p-arvon sitten täytyy olla, jotta nollahypoteesi voidaan hylätä? Yleisimmin käytetty raja on 0,05 eli 5 %. Tämä on kuitenkin täysin mielivaltainen raja ja tapauskohtaista harkintaa on syytä käyttää. Kovin korkealle rajaa ei kuitenkaan voi nostaa. Tämän ymmärtää hyvin vertaamalla tilannetta oikeudenkäyntiin. Tuskin henkilöä päätetään tuomita, jos päätökseen liittyvä erehtymisriski on esimerkiksi 30 %. Oikeudenkäynnissä tilanne on käytännössä hankalampi, koska p-arvon kaltaista todennäköisyyttä ei yleensä ole laskettavissa.

On tärkeää huomata, että tilastollisessa testauksessa ei koskaan osoiteta nollahypoteesia oikeaksi. Todisteet joko riittävät nollahypoteesin hylkäämiseen tai eivät riitä. Vaikka todisteet eivät riitäkään nollahypoteesin hylkäämiseen, niin käytössä ei ole todisteita, jotka osoittaisivat nollahypoteesin oikeaksi. Vähän vastaavalla tavalla voidaan ajatella oikeudenkäynnistäkin. Vaikka todisteet eivät olekaan riittävät syyllisyyden osoittamiseksi, niin eivät ne toisaalta vastaansanomattomasti todista syytetyn syyttömyyttäkään.

On tärkeää huomata, että tilastollisessa testauksessa ei koskaan osoiteta nollahypoteesia oikeaksi.

P-arvoon viittaan artikkeleissani:

• Keskiarvon virhemarginaali – lisätietoa
• Ristiintaulukointi ja khiin neliö -testi
• SPSS: Khiin neliö -testi
• Korrelaatio ja sen merkitsevyys
• Kahden riippumattoman otoksen vertailu
• SPSS: Kahden riippumattoman otoksen vertailu
• Kahden riippuvan otoksen vertailu
• SPSS: Kahden riipuvan otoksen vertailu
• Mann-Whitney U-testi
• Wilcoxon merkittyjen sijalukujen testi
• Kruskal-Wallis -testi
• McNemar-testi
• Yksisuuntainen varianssianalyysi
• SPSS: Yksisuuntainen varianssianalyysi
• Toistomittausten varianssianalyysi
• Friedman-testi

Korrelaatio ja sen merkitsevyys

Päivitetty 17.4.2019. Tämä on Akin menetelmäblogin luetuin artikkeli!

Hallitset jo toivottavasti ristiintaulukoinnin. Ristiintaulukointi on sopiva menetelmä kahden kategorisen muuttujan riippuvuuden tarkasteluun. Kahden määrällisen muuttujan riippuvuutta puolestaan tarkastellaan hajontakaavion ja korrelaatiokertoimen avulla.

Hajontakaavio

Käytän esimerkkinä tiedostosta korrelaatio.xlsx löytyvää dataa, jossa on kolme muuttujaa: opiskelijan läsnäolo lähiopetustunneilla, suoritettujen harjoitustehtävien lukumäärä ja tentin pistemäärä. Haluan selvittää onko lähiopetustunneille osallistumisella ja suoritettujen harjoitustehtävien lukumäärällä yhteyttä tenttipistemäärään.

Saan havainnollisen kuvan asiasta tekemällä hajontakaaviot. Excelissä hajontakaavio on nimeltään Scatter (Piste). Läsnäolon ja tenttipisteiden välisessä hajontakaaviossa en näe merkittävää yhteyttä, vaan havaintopisteet ovat melko satunnaisesti jakautuneet.

Suoritetut harjoitustehtävät sen sijaan näyttävät olevan positiivisessa yhteydessä tenttipistemäärään. Hajontakaaviossa tämä näkyy selvästi nousevana pisteparvena. Alhaiset harjoitustehtävien määrät näyttävät liittyvän alhaisiin tenttipistemääriin ja korkeat harjoitustehtävien määrät näyttävät liittyvän korkeisiin tenttipistemääriin.

Korrelaatiokerroin

Korrelaatiokerroin on tunnusluku suoraviivaisen riippuvuuden voimakkuudelle. Excelissä voin laskea korrelaation funktiolla CORREL (KORRELAATIO). Funktion ensimmäiseksi lähtötiedoksi annetaan viittaus ensimmäisen muuttujan arvoihin ja toiseksi lähtötiedoksi viittaus toisen muuttujan arvoihin.

Korrelaatiokertoimen arvo voi olla mitä tahansa -1 ja +1 väliltä. Lähellä nollaa olevat kertoimet liittyvät tilanteisiin, joissa ei ole suoraviivaista riippuvuutta. Lähellä +1 olevat kertoimet viittaavaat positiiviseen riippuvuuteen (nouseva pisteparvi hajontakaaviossa) ja lähellä -1 olevat kertoimet viittaavat negatiiviseen riippuvuuteen (laskeva pisteparvi hajontakaaviossa).

Esimerkkidatassa läsnäolon ja tenttipistemäärän välinen korrelaatiokerroin on 0,27 ja harjoitusten ja tenttipistemäärän välinen korrelaatiokerroin on 0,84. Korrelaatiokertoimet siis kertovat samaa kuin hajontakaaviot.

Korrelaation merkitsevyys

Jos data pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Korrelaation tapauksessa tämä tarkoittaa muuttujien välisen korrelaation yleistämistä perusjoukkoon.

Pienet korrelaatiot voin selittää otantavirheellä. Otoksessa havaitun korrelaation täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Suuruutta testaan vertaamalla korrelaatiokerrointa hypoteettiseen tilanteeseen, jossa ei ole lainkaan korrelaatiota (korrelaatiokerroin on 0). Jos otoksesta laskettu korrelaatiokerroin poikkeaa riittävästi nollasta, niin voin kutsua korrelaatiota tilastollisesti merkitseväksi.

Korrelaatiokertoimen merkitsevyyden testaamiseksi lasketaan niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: kuinka todennäköistä on saada havaitun suuruinen tai vielä kauempana nollasta oleva korrelaatiokertoimen arvo ilman että korrelaatiota on perusjoukossa? Mitä pienempi p-arvo on sitä enemmän korrelaation yleistäminen perusjoukkoon saa tukea.

Vakiintuneen tavan mukaisesti alle 0,05 (5 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa esiintyvän korrelaation puolesta.

Jos haluat tietää p-arvon laskentaperusteesta, niin lue artikkeli Korrelaatio – lisätietoa.

Voit käyttää p-arvon laskemiseen valmista laskentapohjaa testaa_korrelaatio.xlsx. Kirjoita laskentapohjaan otoskoko ja korrelaatiokerroin, jonka jälkeen voit lukea p-arvon. Käytä 2-suuntaista p-arvoa, jos testaat sitä onko korrelaatio nollasta poikkeava. Käytä 1-suuntaista p-arvoa, jos testaat pelkästään korrelaation positiivisuutta tai pelkästään korrelaation negatiivisuutta.

Jos testaan läsnäolotuntien ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,143 (otoskoko 17, korrelaatiokerroin 0,2746). Tuloksen voin raportoida esimerkiksi seuraavasti (yleisesti käytössä oleva merkintä korrelaatiokertoimelle on r):

Läsnäolotuntien ja tenttipistemäärän välillä ei ole tilastollisesti merkitsevää positiivista korrelaatiota (r=0,27; n=17; 1-suuntaisen testin p-arvo=0,143).

Jos testaan suoritettujen harjoitusten ja tenttipistemäärän välisen korrelaation positiivisuutta, niin saan 1-suuntaiseksi p-arvoksi 0,000 (otoskoko 17, korrelaatiokerroin 0,8438). Tuloksen voin raportoida esimerkiksi seuraavasti:

Suoritettujen harjoitusten ja tenttipistemäärän välillä on positiivinen korrelaatio (r=0,84; n=17; 1-suuntaisen testin p-arvo<0,001).

Tilastollisen merkitsevyyden ohella kannattaa pohtia myös käytännön merkitsevyyttä. Korrelaatiokerroin voi olla tilastollisesti merkitsevä ja silti vailla käytännön merkitsevyyttä. Yksinkertainen tapa käytännön merkitsevyyden arviointiin on hajontakaavion tarkastelu. Jos et näe hajontakaavion pisteparvessa merkittävää säännönmukaisuutta niin saattaa olla että korrelaatiolla ei ole käytännön merkitsevyyttä.

Poikkeavat arvot

Hajontakaaviossa selvästi muista poikkeavat pisteet ovat ongelmallisia korrelaatiokerrointa käytettäessä. Lue lisää artikkelista Poikkeavat arvot.

Lisätietoa

Artikkelissa Korrelaatiokerroin – lisätietoa on yksityiskohtaisempaa tietoa korrelaatiokertoimen laskennasta, p-arvon laskennasta ja ohje korrelaatiokertoimen luottamusvälin laskentaan.

SPSS

SPSS tulostaa korrelaatiokerrointen yhteyteen automaattisesti p-arvot. Lue lisää SPSS monisteesta spss19.pdf.

Ristiintaulukointi ja khiin neliö -testi

Päivitetty 17.4.2019.

Jos datani pohjautuu laajemmasta perusjoukosta satunnaisesti valittuun otokseen, niin tietyin edellytyksin voin yleistää otoksen tuloksia perusjoukkoon. Ristiintaulukoinnin tapauksessa tämä tarkoittaa taulukossa havaitun riippuvuuden tai ryhmien välisen eron yleistämistä perusjoukkoon.

Otoksessa havaitun riippuvuuden tai ryhmien välisen eron täytyy olla riittävän suuri, jotta voin yleistää sen perusjoukkoon. Jos riippuvuus tai ryhmien välinen ero on pieni, niin tämän voin selittää otantavirheellä. Riippuvuuden tai eron suuruutta testaan vertaamalla hypoteettiseen tilanteeseen, jossa ei ole lainkaan riippuvuutta tai lainkaan eroja ryhmien välillä. Vertailun toteuttamiseksi lasken ristiintaulukoinnin rinnalle toisen ristiintaulukoinnin, joka vastaa hypoteettista tilannetta.

Tärkeää: Vaikka ristiintaulukoinnissa on havainnollisempaa esittää prosentit kuin lukumäärät, niin khiin neliö -testauksen lähtökohtana käytetään aina lukumääriä.

Hypoteettisen ristiintaulukoinnin laskeminen

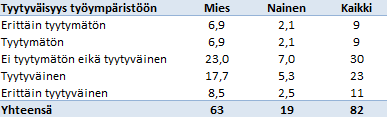
Käytän seuraavassa esimerkkidataa data1.xlsx. Datasta laskettu sukupuolen ja tyytyväisyys työympäristöön välinen ristiintaulukointi näyttää seuraavalta:

Taulukossa on havaittavissa ero miesten ja naisten mielipiteissä (naiset tyytyväisempiä). Eron suuruuden selville saamiseksi lasken hypoteettisen ristiintaulukoinnin, jossa eroa ei ole. Hypoteettisessa taulukossa miesten ja naisten yhteismäärien pitää olla havaitun taulukon mukaiset samoin eri mielipiteitä omaavien yhteismäärät.

Hypoteettisen taulukon lukumäärät saan kertomalla havaitun taulukon rivi- ja sarakesummat keskenään ja jakamalla kokonaissummalla (82). Esimerkiksi erittäin tyytymättömien miesten lukumääräksi saan  (9*63)/82 eli noin 6,9. Laskentamenetelmä perustuu todennäköisyyslaskentaan:

• Jos erittäin tyytymättömiä on 9, niin todennäköisyys sille että otoksesta sattumanvaraisesti valittu on erittäin tyytymätön on 9/82.
• Jos miehiä on 63, niin todennäköisyys sille että otoksesta sattumanvaraisesti valittu on mies on 63/82.
• Todennäköisyyden sille että otoksesta sattumanvaraisesti valittu on erittäin tyytymätön mies saan kertomalla todennäköisyydet 9/82 ja 63/82 keskenään. Kyseinen todennäköisyys kertoo samalla erittäin tyytymättömien miesten prosenttiosuuden siinä tapauksessa että miesten ja naisten mielipiteillä ei ole eroa.
• Laskemalla erittäin tyytymättömien miesten lukumäärä erittäin tyytymättömien miesten prosenttiosuutta käyttäen saan (9/82)*(63/82)*82. Sievennyksen jälkeen tästä tulee (9*63)/82.

Jos lasken taulukon muihin soluihin lukumäärät vastaavalla tavalla (rivisumman ja sarakesumman tulo jaettuna kokonaissummalla), niin saan seuraavan taulukon:

Taulukon lukumääriä kutsutaan odotetuiksi lukumääriksi tai odotetuiksi frekvensseiksi (expected frequencies) ja ne siis vastaavat hypoteettista tilannetta, jossa sukupuolen ja mielipiteen välillä ei ole riippuvuutta (miesten ja naisten mielipiteissä ei ole eroa).

Testin käyttöedellytykset

Havaitun taulukon ja hypoteettisen taulukon eron testaaminen ei ole luotettavaa, jos hypoteettisen taulukon lukumäärät eli odotetut frekvenssit ovat liian pieniä. Kirjallisuudessa annetaan hieman toisistaan poikkeavia rajoja sille, milloin testaaminen muuttuu epäluotettavaksi. Monissa lähteissä esitetään seuraavat kriteerit testaamisen luotettavuudelle:

• Taulukossa, jossa on kaksi riviä ja kaksi saraketta (2×2 taulukko) ei saa olla yhtään alle viiden (5) suuruista odotettua frekvenssiä.
• Suuremmissa taulukoissa alle viiden (5) suuruisia odotettuja frekvenssejä saa olla viidesosa (20 %) kaikista odotetuista frekvensseistä. Alle yhden (1) suuruisia odotettuja frekvenssejä ei saa olla lainkaan.

Edellä lasketussa taulukossa on kolme alle viiden suuruista odotettua frekvenssiä eli 3/10=30 % kaikista. Tämä on liikaa.

Esimerkissäni voin luontevasti yhdistää mielipiteitä (erittäin tyytymätön ja tyytymätön yhteen sekä erittäin tyytyväinen ja tyytyväinen yhteen). Näin taulukko pienenee 5×2 taulukosta 3×2 taulukoksi, jolloin taulukon lukumäärät kasvavat. Esimerkissäni mielipiteiden yhdistäminen korjaa tilanteen eikä alle viiden suuruisia odotettuja frekvenssejä ole kuin 1 (1/6 eli 17 % kaikista).

Khiin neliö Χ²

Havaitun ja hypoteettisen taulukon eroa voin mitata khiin neliö -testimuuttujalla. Khiin neliön merkkinä käytetään kreikkalaista isoa khi-kirjainta varustettuna yläindeksillä 2 (Χ²). Khi-kirjaimen sijasta voin käyttää myös isoa X-kirjainta. En selitä tässä khiin neliö -testimuuttujan laskemista, mutta halutessasi voit lukea testimuuttujan laskemisesta ja khiin neliö -jakaumasta artikkelista Khiin neliö -testi – lisätietoa.

Khiin neliö -testimuuttujan tiedetään noudattavan likimain khiin neliö -todennäköisyysjakaumaa, jonka tarkka muoto riippuu vapausasteluvusta df (degrees of freedom). Vapausasteita on (rivien määrä-1)×(sarakkeiden määrä-1). Esimerkiksi 2×2 taulukossa df=(2-1)×(2-1)=1. Tämän voi ymmärtää helposti: Jos taulukon rivi- ja sarakesummat ovat tiedossa, niin ainoastaan yhden arvon voi asettaa 2×2 taulukkoon vapaasti; muut arvot määräytyvät tämän perusteella.

Khiin neliö -testi

Khiin neliö -testissä määritetään khiin neliö -todennäköisyysjakaumasta niin kutsuttu p-arvo, joka vastaa seuraavaan kysymykseen: Kuinka todennäköistä on saada havaitun suuruinen tai vielä suurempi khiin neliö -testimuuttujan arvo ilman riippuvuutta tai eroa perusjoukossa? Mitä pienempi p-arvo on, sitä enemmän riippuvuuden tai eron yleistäminen perusjoukkoon saa tukea. Toisaalta, mitä suurempi p-arvo on, sitä todennäköisemmin havaitut erot johtuvat otantavirheestä.

Vakiintuneen tavan mukaan alle 0,050 (5,0 %) suuruista p-arvoa pidetään riittävänä näyttönä perusjoukossa olevan riippuvuuden tai eron puolesta.

Excelissä voin laskea p-arvon CHISQ.TEST (CHINELIÖ.TESTI) -funktiolla. Funktiolle annetaan kaksi argumenttia: viittaus havaittuihin frekvensseihin ja viittaus odotettuihin frekvensseihin. Excel 2007 ja vanhemmissa versioissa funktion nimi on CHITEST (CHITESTI). Vanha funktion nimi toimii edelleen myös uudemmissa versioissa.

Khiin neliö -testin raportointi

Esimerkissäni mielipiteiden yhdistämisen jälkeen laskettu khiin neliö -testi antaa p-arvoksi 0,005. Tuloksen voin raportoida esimerkiksi seuraavasti: Miesten ja naisten mielipiteissä on merkitsevää eroa (khiin neliö -testin p-arvo 0,005). Tieteellisessä tekstissä tulos on hyvä raportoida vieläkin täsmällisemmin ilmoittamalla vapausasteiden lukumäärä (df) ja khiin neliö -testimuuttujan arvo: Khiin neliö -testin mukaan miesten (n=63) ja naisten (n=19) mielipiteissä on eroa: df=2; Χ²(2)=10,59; p=0,005.

Excel laskee puolestasi

Onneksi jaksoit lukea tänne asti. Kaikkea ei tarvitse laskea alusta alkaen. Voit käyttää rakentamiani taulukkopohjia otantavirhe.xlsx, joihin voit kirjoittaa tai kopioida oman taulukkosi lukumäärät. Tämän jälkeen näet suoraan odotetut frekvenssit, khiin neliön Χ², vapausasteiden lukumäärän df ja p-arvon. Sinun tehtäväksesi jää tulosten raportointi.

Jos haluat laskea khiin neliö -testin SPSS:llä, niin lue artikkeli SPSS: Khiin neliö -testi.

Yhteenveto

Jos otoksesta lasketussa ristiintaulukoinnissa näkyy ryhmien välisiä eroja, niin

• Mitä pienempi p-arvo, sitä enemmän saan tukea väitteelle, että myös perusjoukossa on ryhmien välisiä eroja. Yleensä alle 0,050 (5,0 %) suuruista p-arvoa pidetään varsin hyvänä tukena väitteelle, että myös perusjoukossa on ryhmien välisiä eroja.
• mitä isompi p-arvo, sitä todennäköisemmin otoksessa havaitut erot johtuvat pelkästään otantavirheestä.

Vaihtoehtoja khiin neliö -testille

Khiin neliö -testi soveltuu käytettäväksi erityisesti kahden kategorisen muuttujan tapauksessa. Jos toinen muuttujista on mielipideasteikollinen, niin Mann-Whitney U -testi (kahden ryhmän vertailu) tai Kruskal-Wallis -testi (useamman ryhmän vertailu) ovat suositeltavampia testimenetelmiä. Tämän artikkelin esimerkissä toisena muuttujana on mielipideasteikollinen muuttuja. Esimerkissä tuleekin ongelmia khiin neliö -testin käyttöedellytysten kanssa. Mann-Whitney U -testissä ei tule ongelmia käyttöedellytysten kanssa. Valitettavasti Excelissä ei ole toimintoa Mann-Whitney U -testin tai Kurskal-Wallis -testin laskemiseen.